题目内容
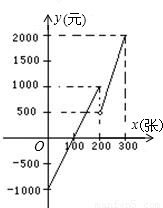
（2005•镇江）某游乐场每天的赢利额y（元）与售出的门票x（张）之间的函数关系如图所示．（1）当0≤x≤200，且x为整数时，y关于x的函数解析式为______；当200≤x≤300，且x为整数时，y关于x的函数解析式为______；
（2）要使游乐场一天的赢利超过1000元，试问该天至少应售出多少张门票；
（3）请思考并解释图象与y轴交点（0，-1000）的实际意义；
（4）根据图象，请你再提供2条信息．
【答案】分析：（1）根据图象可找到点，通过点的坐标可求出两段的解析式，都是一次函数．
（2）通过观察可知，应该是y＞1000，应该用第二段．
（3）如果有一天的门票为0的话，游乐园就会亏损1000元．如果一天卖出100张门票，则游乐场不盈利也不亏损；买200张门票时，还是采用0≤x≤200，游乐场会盈利1000元．
解答：解：（1）设0≤x≤200时，y=kx-1000，把（100，0）代入可得：0=100k-1000，解得，k=10，那么可得函数式为：y=10x-1000．设第二段范围的函数式为：y=kx+b，把（200，500）和（300，2000）代入可得：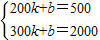
，解得
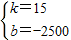即y=15x-2500；
（2）∵y＞1000，那么根据图象，则15x-2500＞1000，解得，x＞
，x取整则x=234（张）．
（3）图象与y轴交点（0，-1000）的实际意义为：当每天不卖门票时，每天亏损1000元．
（4）答案不唯一，合理即可．
点评：能看懂图象的意思，并使用了待定系数法求函数解析式．还运用了解一元一次不等式的内容．
（2）通过观察可知，应该是y＞1000，应该用第二段．
（3）如果有一天的门票为0的话，游乐园就会亏损1000元．如果一天卖出100张门票，则游乐场不盈利也不亏损；买200张门票时，还是采用0≤x≤200，游乐场会盈利1000元．
解答：解：（1）设0≤x≤200时，y=kx-1000，把（100，0）代入可得：0=100k-1000，解得，k=10，那么可得函数式为：y=10x-1000．设第二段范围的函数式为：y=kx+b，把（200，500）和（300，2000）代入可得：
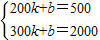，解得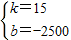即y=15x-2500；（2）∵y＞1000，那么根据图象，则15x-2500＞1000，解得，x＞
，x取整则x=234（张）．（3）图象与y轴交点（0，-1000）的实际意义为：当每天不卖门票时，每天亏损1000元．
（4）答案不唯一，合理即可．
点评：能看懂图象的意思，并使用了待定系数法求函数解析式．还运用了解一元一次不等式的内容．
练习册系列答案
相关题目
