题目内容
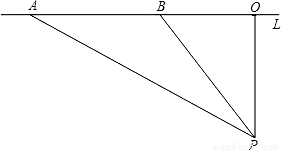
如图，已知测速站P到公路L的距离PO为40米，一辆汽车在公路L上行驶，测得此车从点A行驶到点B所用的时间为2秒，并测得∠APO=60°
，∠BPO=30°，计算此车从A到B的平均速度为每秒多少米（结果保留四个有效字），并判断此车是否超过了每秒22米的限制速度？
分析：在直角三角形POB中，∠BPO=30°，PO=40，利用30°的正切值可得BO长，同理可得到AO长，减去BO长，除以时间即为汽车速度，跟22比较即可．
解答：解：∵在直角三角形POB中，∠BPO=30°，PO=40
∴BO=OP×tan30°=
同理可得OA=40
那么AB=OA-OB=
米
速度为
÷2=
≈23.09米/秒，
∴超过了22米/秒的限制速度．
∴BO=OP×tan30°=
40
| ||
| 3 |
同理可得OA=40
| 3 |
那么AB=OA-OB=
80
| ||
| 3 |
速度为
80
| ||
| 3 |
40
| ||
| 3 |
∴超过了22米/秒的限制速度．
点评：解决本题的关键是利用直角三角形的三角函数求得2秒内走过的路程．
练习册系列答案
阅读快车系列答案
相关题目
，∠BPO=30°，计算此车从A到B的平均速度为每秒多少米（结果保留四个有效字），并判断此车是否超过了每秒22米的限制速度？
