题目内容
(1)画图,已知线段a和锐角∠α,求作Rt△ABC,使它的一边为a,一锐角为∠α(不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可).(2)回答问题:
①满足上述条件的大小不同的共有
②若∠α=30°,求最大的Rt△ABC的面积.
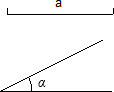
分析:(1)截取AB=a,过B作CB⊥AB,即可;
(2)根据①中a,可以作为斜边和两条直角边中任意一条,即可得出答案,
②只有∠α=30°所对边是a时,此时面积最大,求出即可.
(2)根据①中a,可以作为斜边和两条直角边中任意一条,即可得出答案,
②只有∠α=30°所对边是a时,此时面积最大,求出即可.
解答:解:(1)如图所示:
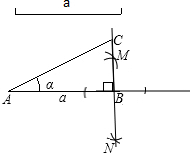
(2)根据①a可以作为斜边和两条直角边中任意一条,
∴满足上述条件的大小不同的共有3种,
故答案为:3;
②∵∠α=30°,
∴最大的Rt△ABC的面积为2a×
a×
=
a2.

(2)根据①a可以作为斜边和两条直角边中任意一条,
∴满足上述条件的大小不同的共有3种,
故答案为:3;
②∵∠α=30°,
∴最大的Rt△ABC的面积为2a×
| 3 |
| 1 |
| 2 |
| 3 |
点评:此题主要考查了过一点作一直线垂直于已知直线以及分类讨论思想的应用,题目综合性较强,考查知识较全面,同学们应认真分析.

练习册系列答案
相关题目
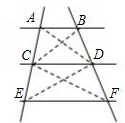 如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究:
如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究: (1)画图,已知线段a和锐角
(1)画图,已知线段a和锐角 2若
2若
 ,求作Rt△ABC,使它的一边为a,一锐角为
,求作Rt△ABC,使它的一边为a,一锐角为 ,求最大的Rt△ABC的面积。
,求最大的Rt△ABC的面积。 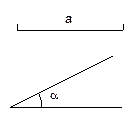
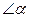 ,求作Rt△ABC,使它的一边为a,一锐角为
,求作Rt△ABC,使它的一边为a,一锐角为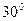 ,求最大的Rt△ABC的面积。
,求最大的Rt△ABC的面积。