Question

补全下列各题解题过程．
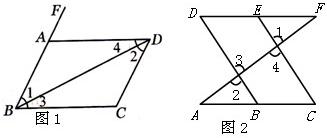
（1）如图1，①∵AD∥BC
∴∠FAD=________．（________）
②∵∠1=∠2
∴________∥________（________）

（2）如图2，E点为DF上的点，B为AC上的点，
∠1=∠2，∠C=∠D，求证DF∥AC．
证明：∵∠1=∠2（已知）
∠2=∠3∠1=∠4 （________）
∴∠3=∠4　（________）
∴________∥________ （________）
∴∠C=∠ABD　（________　）
∵∠C=∠D　　（________　）
∴∠D=∠ABD（________）
∴DF∥AC（________）

Answer 1

解：
（1）如图1，①∵AD∥BC
∴∠FAD=∠ABC．（ 两直线平行，同位角相等）
②∵∠1=∠2
∴AB∥CD（ 内错角相等，两直线平行）

（2）如图2，E点为DF上的点，B为AC上的点，
∠1=∠2，∠C=∠D，求证DF∥AC．
证明：∵∠1=∠2（已知）
∠2=∠3∠1=∠4 （ 对顶角相等）
∴∠3=∠4 （ 等量代换）
∴DB∥CE （ 内错角相等，两直线平行）
∴∠C=∠ABD （ 两直线平行，同位角相等　）
∵∠C=∠D （ 已知　）
∴∠D=∠ABD（ 等量代换）
∴DF∥AC（ 内错角相等，两直线平行）．
故答案为：（1）∠ABC，两直线平行，同位角相等，AB，CD，内错角相等，两直线平行，（2）对顶角相等，等量代换，DB，CE，内错角相等，两直线平行，两直线平行，同位角相等，已知，等量代换，内错角相等，两直线平行，
分析：（1）①由平行，得到同位角相等；②由∠1=∠2，根据平行线的判定得到平行；
（2）由∠1=∠2推出∠3=∠4，进一步推出DB和CE平行，得到∠D和∠ABD相等，即可推出DF和AC平行．
点评：本题主要考查了平行线的性质和判定，对顶角的性质等知识点，解此题的关键是灵活运用平行线的性质和判定进行证明．