ЬтФПФкШн
ЁОЬтФПЁПвбжЊ ![]() жаЃЌ
жаЃЌ ![]() .Еу
.Еу ![]() ДгЕу
ДгЕу ![]() ГіЗЂбиЯпЖЮ
ГіЗЂбиЯпЖЮ ![]() вЦЖЏЃЌЭЌЪБЕу
вЦЖЏЃЌЭЌЪБЕу ![]() ДгЕу
ДгЕу ![]() ГіЗЂбиЯпЖЮ
ГіЗЂбиЯпЖЮ ![]() ЕФбгГЄЯпвЦЖЏЃЌЕу
ЕФбгГЄЯпвЦЖЏЃЌЕу ![]() ЁЂ
ЁЂ ![]() вЦЖЏЕФЫйЖШЯрЭЌЃЌ
вЦЖЏЕФЫйЖШЯрЭЌЃЌ ![]() гыжБЯп
гыжБЯп ![]() ЯрНЛгкЕу
ЯрНЛгкЕу ![]() .
.
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕу ![]() ЮЊ
ЮЊ ![]() ЕФжаЕуЪБЃЌЧѓ
ЕФжаЕуЪБЃЌЧѓ ![]() ЕФГЄЃЛ
ЕФГЄЃЛ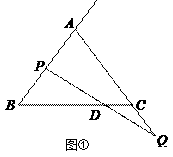
ЃЈ2ЃЉШчЭМЂкЃЌЙ§Еу ![]() зїжБЯп
зїжБЯп ![]() ЕФДЙЯпЃЌДЙзуЮЊ
ЕФДЙЯпЃЌДЙзуЮЊ ![]() ЃЌЕБЕу
ЃЌЕБЕу ![]() ЁЂ
ЁЂ ![]() дквЦЖЏЕФЙ§ГЬжаЃЌЩш
дквЦЖЏЕФЙ§ГЬжаЃЌЩш ![]() ЃЌ
ЃЌ ![]() ЪЧЗёЮЊГЃЪ§ЃПШєЪЧЧыЧѓГі
ЪЧЗёЮЊГЃЪ§ЃПШєЪЧЧыЧѓГі ![]() ЕФжЕЃЌШєВЛЪЧЧыЫЕУїРэгЩ.
ЕФжЕЃЌШєВЛЪЧЧыЫЕУїРэгЩ.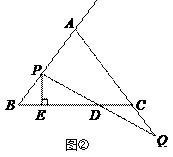
ЃЈ3ЃЉШчЭМЂлЃЌEЮЊBCЕФжаЕуЃЌжБЯпCHДЙжБгкжБЯпADЃЌДЙзуЮЊЕуHЃЌНЛAEЕФбгГЄЯпгкЕуMЃЛжБЯпBFДЙжБгкжБЯпADЃЌДЙзуЮЊFЃЛевГіЭМжагыBDЯрЕШЕФЯпЖЮЃЌВЂжЄУї.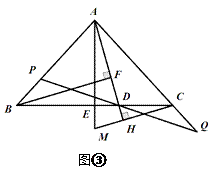
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКШчЭМЃЌЙ§PЕузїPFЁЮACНЛBCгкFЃЌ
ЁпЕуPКЭЕуQЭЌЪБГіЗЂЃЌЧвЫйЖШЯрЭЌЃЌ
ЁрBP=CQЃЌ
ЁпPFЁЮAQЃЌ
ЁрЁЯPFB=ЁЯACBЃЌЁЯDPF=ЁЯCQDЃЌ
гжЁпAB=ACЃЌ
ЁрЁЯB=ЁЯACBЃЌ
ЁрЁЯB=ЁЯPFBЃЌ
ЁрBP=PFЃЌ
ЁрPF=CQЃЌгжЁЯPDF=ЁЯQDCЃЌ
ЁрЁїPFDЁеЁїQCDЃЌ
ЁрDF=CD= ![]() CFЃЌ
CFЃЌ
гжвђPЪЧABЕФжаЕуЃЌPFЁЮAQЃЌ
ЁрFЪЧBCЕФжаЕуЃЌМДFC= ![]() BC=6ЃЌ
BC=6ЃЌ
ЁрCD= ![]() CF=3
CF=3
ЃЈ2ЃЉНтЃК ![]() ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ШчЭМЂкЃЌЕуPдкЯпЖЮABЩЯЃЌЙ§ЕуPзїPFЁЮACНЛBCгкFЃЌ
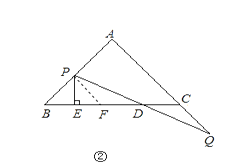
взжЊЁїPBFЮЊЕШбќШ§НЧаЮЃЌ
ЁпPEЁЭBF
ЁрBE= ![]() BF
BF
ЁпвзЕУЁїPFDЁеЁїQCD
ЁрCD= ![]()
Ёр ![]()
ЃЈ3ЃЉНтЃКBD=AM
жЄУїЃКЁп ![]()
Ёр ![]()
Ёр ![]()
ЁпEЮЊBCЕФжаЕу
Ёр ![]()
Ёр ![]() ,
, ![]()
Ёр ![]() ЃЌ
ЃЌ ![]()
ЁпAHЁЭCM
Ёр ![]()
Ёп ![]()
Ёр ![]()
Ёр ![]() Ёе
Ёе ![]() (ASA)
(ASA)
Ёр ![]()
Ёр ![]()
МДЃК ![]()
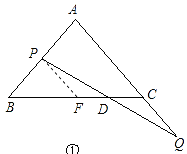
ЁОНтЮіЁПЃЈ1ЃЉИљОнвбжЊПЩжЊBP=CQЃЌдйИљОнPFЁЮAQМАAB=ACЃЌжЄУїЁЯB=ЁЯPFBЃЌЕУГіBP=PFЃЌжЄЕУPF=CQЃЌШЛКѓИљОнНЧНЧБпжЄУїЁїPFDЁеЁїQCDЃЌЕУГіDF=CD=![]() CFЃЌИљОнвбжЊPЪЧABЕФжаЕуЃЌPFЁЮAQЃЌжЄУїЕуFЪЧBCЕФжаЕуЃЌЧѓГіCFЕФГЄЃЌМДПЩЧѓГіCDЕФГЄЁЃ
CFЃЌИљОнвбжЊPЪЧABЕФжаЕуЃЌPFЁЮAQЃЌжЄУїЕуFЪЧBCЕФжаЕуЃЌЧѓГіCFЕФГЄЃЌМДПЩЧѓГіCDЕФГЄЁЃ
ЃЈ2ЃЉЕуPдкЯпЖЮABЩЯЃЌЙ§ЕуPзїPFЁЮACНЛBCгкFЃЌЯШжЄУїЁїPBFЮЊЕШбќШ§НЧаЮЃЌИљОнPEЁЭBFЃЌЕУГіBEгыЯпЖЮBFЕФЪ§СПЙиЯЕЃЌдйжЄУїЁїPFDЁеЁїQCD ЃЌНсКЯCD= ![]() C FЃЌШЛКѓИљОнB E + C D =
C FЃЌШЛКѓИљОнB E + C D =![]() BCЃЌМДПЩЕУГіНсТлЁЃ
BCЃЌМДПЩЕУГіНсТлЁЃ
ЃЈ3ЃЉЯШИљОнЙДЙЩЖЈРэЕФФцЖЈРэжЄУїІЄABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ дйИљОнEЮЊBCЕФжаЕуЃЌШЅжЄУїAE=ECЃЌЁЯEAD = ЁЯECMЃЌШЛКѓжЄУїЁїAEDЁеЁїCEMЃЌЕУГіDE=MEЃЌИљОнBD=DE+BE=AE+ME=AMЁЃМДПЩЕУГіНсТлЁЃ

 КшЭМЭМЪщКЎМйзївЕМйЦкзївЕМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
КшЭМЭМЪщКЎМйзївЕМйЦкзївЕМЊСжДѓбЇГіАцЩчЯЕСаД№АИЁОЬтФПЁПЁАСЋГЧЖСЪщдТЁБЛюЖЏНсЪјКѓЃЌЖдАЫФъМЖЃЈШ§ЃЉАр45ШЫЫљдФЖСЪщМЎЪ§СПЧщПіЕФЭГМЦНсЙћШчЯТБэЫљЪОЃК
дФЖСЪ§СП | 1БО | 2БО | 3БО | 3БОвдЩЯ |
ШЫЪ§ЃЈШЫЃЉ | 10 | 18 | 13 | 4 |
ИљОнЭГМЦНсЙћЃЌдФЖС2БОЪщМЎЕФШЫЪ§зюЖрЃЌетИіЪ§Он2ЪЧЃЈ ЃЉ
AЃЎЦНОљЪ§ BЃЎжаЮЛЪ§ C.жкЪ§ DЃЎЗНВю