Question

等腰梯形的上底与腰相等，下底与对角线相等，则梯形较小的底角度数是________．

Answer 1

72°
分析：根据已知条件“上底与腰相等”和“下底与对角线相等”分别推知∠ADB=∠ABD=∠2、∠DCB=∠DBC=∠1；然后由等腰梯形的两个底角相等、两直线平行，同旁内角互补知180°-2∠1+∠2=∠1和2∠1+∠2=180°，结合这两个算式求∠1的度数即可．
解答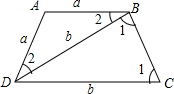：解：根据题意，知
AB=AD，
∴∠ADB=∠ABD=∠2；
又∵BD=DC，
∴∠DCB=∠DBC=∠1；
又由∠1+∠1+∠2=180°（两直线平行，同旁内角互补），
∴2∠1+∠2=180°；①
∵四边形ABCD是等腰梯形，
∴180°-2∠1+∠2=∠1（等腰梯形的两个底角相等）；②
由①②，得
∠1=72°；
∴梯形较小的底角度数是72°．
故答案是：72°．
点评：本题考查了等腰梯形的性质．解答本题时，利用了“等腰梯形的两个底角相等”的性质．