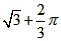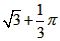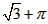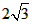题目内容
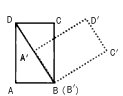
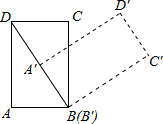 如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=
如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD= ,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为
,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为
(注解:所谓画刷,是屏幕上的一个矩形块,它在屏幕上移动或转动时,它扫过的部位将改变颜色.)
- A.
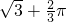
- B.
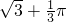
- C.
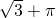
- D.

A
分析:首先理解题干条件可知这个画刷所着色的面积=2S△ABD+S扇形,扇形的圆心角为60°,半径为2,求出扇形面积和三角形的面积即可.
解答:根据题意可知:
这个画刷所着色的面积=2S△ABD+S扇形,
S△ABD= ×
× =
= ,
,
在Rt△ABD中,
∵AB=1,AD= ,根据勾股定理得:BD=2,
,根据勾股定理得:BD=2,
∴AB= BD,
BD,
∴∠ADB=30°,则∠ABD=60°,
连接BD′,则∠DBD′=60°,
S扇形=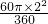 =
=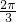 ,
,
∴这个画刷所着色的面积=2S△ABD+S扇形= +
+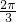 .
.
故选A.
点评:本题主要考查扇形面积的计算和旋转的性质的知识点,解答本题的关键是理解着色的面积等于一个扇形面积和一个三角形面积之和,此题难度不大.
分析:首先理解题干条件可知这个画刷所着色的面积=2S△ABD+S扇形,扇形的圆心角为60°,半径为2,求出扇形面积和三角形的面积即可.
解答:根据题意可知:
这个画刷所着色的面积=2S△ABD+S扇形,
S△ABD=
 ×
× =
= ,
,在Rt△ABD中,
∵AB=1,AD=
 ,根据勾股定理得:BD=2,
,根据勾股定理得:BD=2,∴AB=
 BD,
BD,∴∠ADB=30°,则∠ABD=60°,
连接BD′,则∠DBD′=60°,
S扇形=
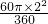 =
=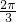 ,
,∴这个画刷所着色的面积=2S△ABD+S扇形=
 +
+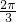 .
.故选A.
点评:本题主要考查扇形面积的计算和旋转的性质的知识点,解答本题的关键是理解着色的面积等于一个扇形面积和一个三角形面积之和,此题难度不大.

练习册系列答案
相关题目
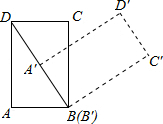 如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=
如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=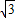 ,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为( )
,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为( )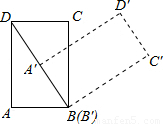
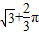
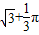

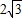
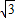 ,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为( )
,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为( )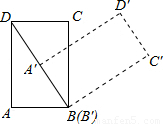
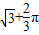
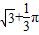
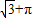
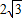
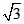 ,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为(注解:所谓画刷,是屏幕上的一个矩形块,它在屏幕上移动或转动时,它扫过的部位将改变颜色。)
,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为(注解:所谓画刷,是屏幕上的一个矩形块,它在屏幕上移动或转动时,它扫过的部位将改变颜色。)