题目内容
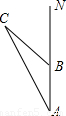
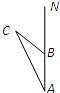 19、地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.
19、地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.(1)求B处到村庄C的距离;
(2)求村庄C到该公路的距离.(结果精确到0.1km)
(参考数据:sin26°≈0.438 4,cos26°≈0.898 8,sin52°≈0.788 0,cos52°≈0.6157)
分析:过C作CD⊥AB,交AB于D,易证△ABC是等腰三角形,在直角△CBD中,根据三角函数就可以求出CD.
解答: 解:过C作CD⊥AB,交AB于D.
解:过C作CD⊥AB,交AB于D.
(1)∵∠CBD=52°,∠A=26°,
∴∠BCA=26°.
∴BC=AB=70.
即B处到村庄C的距离为70km.
(2)在Rt△CBD中,CD=CB×sin52°=70×0.7880≈55.2,
即村庄C到该公路的距离约为55.2km.
 解:过C作CD⊥AB,交AB于D.
解:过C作CD⊥AB,交AB于D.(1)∵∠CBD=52°,∠A=26°,
∴∠BCA=26°.
∴BC=AB=70.
即B处到村庄C的距离为70km.
(2)在Rt△CBD中,CD=CB×sin52°=70×0.7880≈55.2,
即村庄C到该公路的距离约为55.2km.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
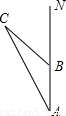 地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.
地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.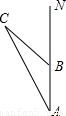 地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.
地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.