题目内容

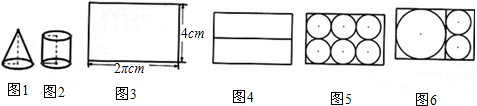
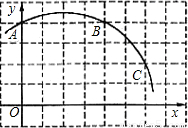
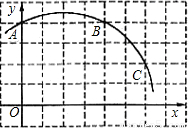
已知一个圆锥和一个圆柱，它们的底面半径相等，高也相等，且圆锥的轴截面是正三角形．则圆柱与圆锥的侧面积之比为

：1

．

分析：设圆锥的底面半径是r，则圆柱的高就是圆锥的高，利用三角函数即可求得，然后求得侧面；圆锥的母线长等于底面直径，然后利用扇形的面积公式即可求得圆锥的侧面积，即可求得二者的比值．

解答：解：设圆锥的底面半径是r，则圆锥的高是

r，
则圆柱的侧面积是：2πr•

r=2

πr²；
圆锥的底面周长是2πr，母线长是2γ，则侧面积是：

×2πr•2r=2πr²．
则圆柱与圆锥的侧面积之比为

：1．
故答案是：

：1．

点评：本题利用了圆锥的计算，圆的周长公式和扇形面积公式求解．注意圆锥表面积=底面积+侧面积=π×底面半径²+底面周长×母线长÷2的应用．

练习册系列答案

1加1阅读好卷系列答案

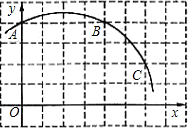如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．
（1）用直尺和圆规画出该圆弧所在圆的圆心M的位置（不用写作法，保留作图痕迹）．
（2）若A点的坐标为（0，4），D点的坐标为（7，0），直线CD与⊙M的位置关系为______，再连接MA、MC，将扇形AMC卷成一个圆锥，求此圆锥的侧面积．

【问题】如图1、2是底面为1cm，母线长为2cm的圆柱体和圆锥体模型．现要用长为2πcm，宽为4cm的长方形彩纸（如图3）装饰圆柱、圆锥模型表面．已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢？
【对话】老师：“长方形纸可以怎么裁剪呢？”
学生甲：“可按图4方式裁剪出2张长方形．”
学生乙：“可按图5方式裁剪出6个小圆．”
学生丙：“可按图6方式裁剪出1个大圆和2个小圆．”
老师：尽管还有其他裁剪方法，但为裁剪方便，我们就仅用这三位同学的裁剪方法！
【解决】（1）计算：圆柱的侧面积是cm²，圆锥的侧面积是cm²．
（2）1张长方形彩纸剪拼后最多能装饰个圆锥模型；5张长方形彩纸剪拼后最多能装饰个圆柱体模型．
（3）求用122张彩纸对多能装饰的圆锥、圆柱模型套数．