题目内容
【题目】如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= . 
【答案】2
【解析】解:作PE⊥OA于E,
∵∠AOP=∠BOP,PD⊥OB,PE⊥OA,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴在Rt△PCE中,PE= ![]() PC=
PC= ![]() ×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),
×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴PD=PE=2,
故答案是:2.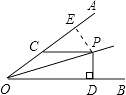
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目