题目内容
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数关系:
(1)求销售量y与销售单价x的函数关系式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;并求出销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价的范围.
| x | … | 60 | 65 | 70 | 75 | 80 | … |
| y | … | 60 | 55 | 50 | 45 | 40 | … |
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;并求出销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价的范围.
(1)设售量y(件)与销售单价x(元)的一次函数关系为y=kx+b(k≠0),
把(60,60)、(80,40)代入,
得
,
解得
,
∴销售量y与销售单价x的函数关系式y=-x+120;
∵成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,即不高于60(1+45%),
∴60≤x≤87;
(2)W=(x-60)•y
=(x-60)(-x+120)
=-x2+180x-7200(60≤x≤87);
W=-(x-90)2+900,
∵a=-1<0,
∴当x<90时,W随x的增大而增大,
∴x=87时,W有最大值,其最大值=-(87-90)2+900=891,
即销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(3)令W=500,则-(x-90)2+900=500,解得x1=70,x2=110,
∵当x<90时,W随x的增大而增大,
∴当销售单价的范围为70(元)≤x≤87(元)时,该商场获得利润不低于500元.
把(60,60)、(80,40)代入,
得
|
解得
|
∴销售量y与销售单价x的函数关系式y=-x+120;
∵成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,即不高于60(1+45%),
∴60≤x≤87;
(2)W=(x-60)•y
=(x-60)(-x+120)
=-x2+180x-7200(60≤x≤87);
W=-(x-90)2+900,
∵a=-1<0,
∴当x<90时,W随x的增大而增大,
∴x=87时,W有最大值,其最大值=-(87-90)2+900=891,
即销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(3)令W=500,则-(x-90)2+900=500,解得x1=70,x2=110,
∵当x<90时,W随x的增大而增大,
∴当销售单价的范围为70(元)≤x≤87(元)时,该商场获得利润不低于500元.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某商场试销一种成本为50元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于50%.经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数关系,试销数据如下表:
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为ω元,试写出利润ω与销售单价x之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
| 售价(元/件) | … | 55 | 60 | 70 | … |
| 销量(件) | … | 75 | 70 | 60 | … |
(2)若该商场获得利润为ω元,试写出利润ω与销售单价x之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
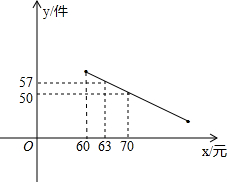 (2012•鄂尔多斯)某商场试销一种成本为每件60元的T恤,规定试销期间销售单价不低于成本单价,且获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)之间的函数图象如图所示:
(2012•鄂尔多斯)某商场试销一种成本为每件60元的T恤,规定试销期间销售单价不低于成本单价,且获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)之间的函数图象如图所示: