题目内容
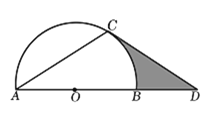
【题目】实践操作如图,∠△ABC是直角三角形,∠ACB=90,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点0
②以点0为圆心,OC为半径作圆.综合运用在你所作的图中,
(1)直线AB与⊙0的位置关系是
(2)证明:BA·BD=BC·BO;
(3)若AC=5,BC=12,求⊙0的半径

【答案】实践操作,作图见解析;综合运用:(1)相切;(2)证明见解析;(3)![]()
【解析】实践操作:根据题意画出图形即可;
综合运用:(1)根据角平分线上的点到角两边的距离相等可得AB与⊙O的位置关系是相切;
(2)证明ΔBOD∽ΔBAC即可;
(3)首先根据勾股定理计算出AB的长,再设半径为x,则OC=OD=x,BO=(12-x)再次利用勾股定理可得方程x2+82=(12-x)2,再解方程即可.
试题解析:实践操作,如图所示:

综合运用:
综合运用:
(1)AB与⊙O的位置关系是相切.
∵AO是∠BAC的平分线,
∴DO=CO,
∵∠ACB=90°,
∴∠ADO=90°,
∴AB与⊙O的位置关系是相切;
(2)∵AB、AC是切线
∴∠BDO=∠BCA=90°
又∠DBC=∠CBA
∴ΔBDO∽ΔCBA
∴![]()
即: ![]()
(3)因为AC=5,BC=12,
所以AD=5,AB=13,
所以DB=13﹣5=7,
设半径为x ,则OC=OD=x ,BO=(12﹣x),
x2+82=(12﹣x)2,
解得:x=![]() .
.
答:⊙O的半径为![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目