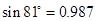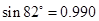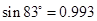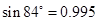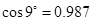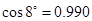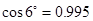题目内容
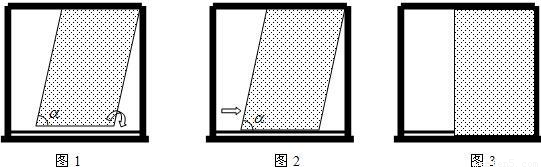
现代家居设计的“推拉式”钢窗,运用了轨道滑行技术,纱窗装卸时利用了平行四边形的不稳定性,操作步骤如下:(1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1);
(2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2);
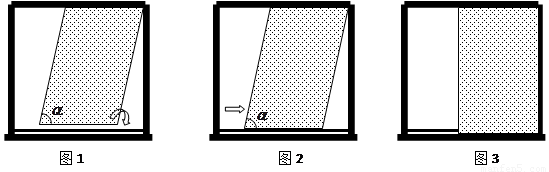
(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).
在装卸纱窗的过程中,如图所示∠α的值不得小于81°,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时∠α的最大整数值.(下表提供的数据可供使用)
| sin81°=0.987 | sin82°=0.990 | sin83°=0.993 | sin84°=0.995 |
| cos9°=0.987 | cos8°=0.990 | cos7°=0.993 | cos 6°=0.995 |
【答案】分析:纱窗的高,平行四边形的斜边,以及∠α正好构成直角三角形,在这个直角三角形中利用三角函数就可以求出高.
解答:解:能够合理装上平行四边形纱窗时的最大高度:96-0.9=95.1(cm),
能够合理装上平行四边形纱窗时的高:96sin∠α或96•cos(90°-∠α).
当∠α=81°时,纱窗高:96sin81°=96×0.987=94.752<95.1∴此时纱窗能装进去;
当∠α=82°时,纱窗高:96sin82°=96×0.990=95.04<95.1∴此时纱窗能装进去;
当∠α=83°时,纱窗高:96sin83°=96×0.993=95.328>95.1∴此时纱窗装不进去.
因此能合理装上纱窗时∠α的最大值是82°.
点评:本题考查了直角三角形的有关知识,构造直角三角形利用直角三角形的性质解题是解决本题关键,此外读懂题目也很重要.
解答:解:能够合理装上平行四边形纱窗时的最大高度:96-0.9=95.1(cm),
能够合理装上平行四边形纱窗时的高:96sin∠α或96•cos(90°-∠α).
当∠α=81°时,纱窗高:96sin81°=96×0.987=94.752<95.1∴此时纱窗能装进去;
当∠α=82°时,纱窗高:96sin82°=96×0.990=95.04<95.1∴此时纱窗能装进去;
当∠α=83°时,纱窗高:96sin83°=96×0.993=95.328>95.1∴此时纱窗装不进去.
因此能合理装上纱窗时∠α的最大值是82°.
点评:本题考查了直角三角形的有关知识,构造直角三角形利用直角三角形的性质解题是解决本题关键,此外读懂题目也很重要.

练习册系列答案
相关题目
现代家居设计的“推拉式”钢窗,运用了轨道滑行技术,纱窗装卸时利用了平行四边形的不稳定性,操作步骤如下:
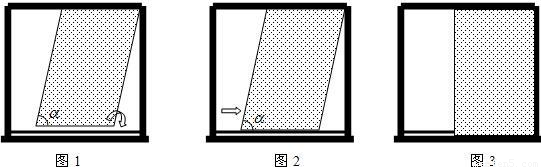
(1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1);
(2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2);
(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).
在装卸纱窗的过程中,如图所示∠α的值不得小于81°,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时∠α的最大整数值.(下表提供的数据可供使用)
(1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1);
(2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2);
(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).
在装卸纱窗的过程中,如图所示∠α的值不得小于81°,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时∠α的最大整数值.(下表提供的数据可供使用)
| sin81°=0.987 | sin82°=0.990 | sin83°=0.993 | sin84°=0.995 |
| cos9°=0.987 | cos8°=0.990 | cos7°=0.993 | cos 6°=0.995 |


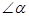 的值不得小于
的值不得小于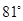 ,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时
,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时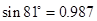
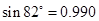
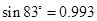
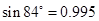
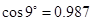
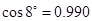
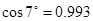
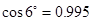

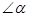 的值不得小于
的值不得小于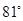 ,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时
,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时