题目内容
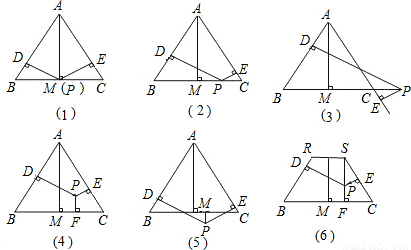
 26、附加题:如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.
26、附加题:如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.(1)求证:AB=AD;
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
分析:(1)连接AC,根据题意易得AE、AF是BC、CD的垂直平分线,可得AB=AC,AD=AC,可证出AB=AD.
(2)根据等腰三角形的性质解答即可.
(2)根据等腰三角形的性质解答即可.
解答: 解:(1)连接AC,
解:(1)连接AC,
∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD.
(2)∠EAF=2∠BAE=2∠DAF.
证明:∵由(1)知AB=AD=AC,
∴△ABC、△ACD为等腰三角形,
∵AE⊥BC,AF⊥CD,
∴∠BAE=∠EAC=∠CAF=∠DAF,
∴∠EAF=2∠BAE=2∠DAF.
 解:(1)连接AC,
解:(1)连接AC,∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD.
(2)∠EAF=2∠BAE=2∠DAF.
证明:∵由(1)知AB=AD=AC,
∴△ABC、△ACD为等腰三角形,
∵AE⊥BC,AF⊥CD,
∴∠BAE=∠EAC=∠CAF=∠DAF,
∴∠EAF=2∠BAE=2∠DAF.
点评:此题考查的是线段的垂直平分线的性质及等腰三角形的性质等几何知识.解答此题的关键是连接AC,构造出等腰三角形.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
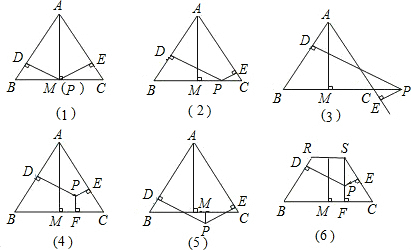
 .图4与图6中的等式有何关系.
.图4与图6中的等式有何关系.
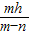 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.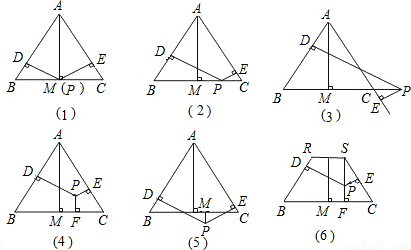
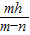 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.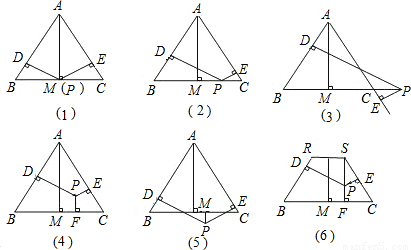
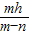 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.