题目内容
【题目】在等边△ABC的外侧作直线BD,作点A关于直线BD的对称点A′,连接AA′交直线BD于点E,连接A′C交直线BD于点F.
(1)依题意补全图1,已知∠ABD=30°,求∠BFC的度数; 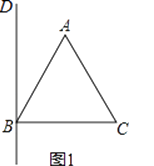
(2)如图2,若60°<∠ABD<90°,判断直线BD和A′C相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由. 
【答案】
(1)解:补全的图1如下所示:
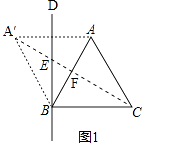
连接BA′,
∵由已知可得,BD垂直平分AA′,∠ABD=30°,△ABC是等边三角形,
∴△BA′A是等边三角形,AA′∥BC且AA′=BC,A′A=A′B,
∴四边形AA′BC是菱形,
∵∠ACB=60°,
∴∠BCE=30°
(2)解:直线BD和A′C相交所成的锐角的度数是定值,若下图所示,
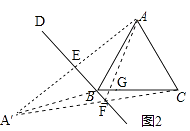
连接AF交BC于点G,
由已知可得,BA′=BA,BA=BC,FA′=FA,
则∠BA′A=∠BAA′,∠FA′A=∠FAA′,BA′=BC,
∴∠BA′C=∠BCA′,∠FA′B=∠FAB,
∴∠BCA′=∠FAB,
∵∠FGC=∠BGA,∠ABC=60°,
∴∠CFA=∠ABC=60°,
∵∠AFC+∠AFD+∠A′FD=180°,∠A′FD=∠AFD,
∴∠A′FD=60°,
即直线BD和A′C相交所成的锐角的度数是定值,这个锐角的度数是60°
【解析】(1)根据题意可以作出相应的图形,连接A′B,由题意可得到四边形AA′BC是菱形,根据菱形的对角线平分每一组对角,可以得到∠BFC的度数;(2)画出相应的图形,根据对称的性质可以得到相等的线段和相等的角,由等边△ABC,可以得到BC=BA,然后根据三角形内角和是180°,可以推出直线BD和A′C相交所成的锐角的度数,本题得以解决.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.

【题目】某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q = W + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
次数n | 2 | 1 |
速度x | 40 | 60 |
指数Q | 420 | 100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.