Question

一个三角形有9条重要线段--3条角平分线、3条中线、3条高线，小军学完了“等腰三角形底边上的中线、高线和顶角角平分线三线合一”的性质后，发现这9条线段变成了7条，进而他又发现在这7条线段中，又存在着三对相等的线段，请你用文字语言叙述小军发现的结论（写出一种即可），并画出图形，写出已知、求证，并且证明它．

Answer 1

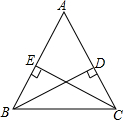解：等腰三角形两腰上的高线相等．
已知：在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E．
求证：BD=CE．
证明：∵BD⊥AC，CE⊥AB，AB=AC，
∴∠BDC=∠BEC=90°，∠ABC=∠ACB，
∵BC=BC，
∴△BEC≌△CDB，
∴BD=CE．
还可证明：等腰三角形两腰上的中线相等，等腰三角形两底角的角平分线相等．
分析：小军还发现存在的三对相等的线段为：等腰三角形两腰上的高线相等；等腰三角形两腰上的中线相等；等腰三角形两底角的角平分线相等；此处只证第一个，如图，根据等腰三角形的性质及已知可利用AAS判定△BEC≌△CDB，根据全等三角形的性质即可得到结论．
点评：此题主要考查等腰三角形的性质及全等三角形的判定与性质的综合运用．