题目内容
给出下列二次函数:①y=x2+2x;②y=-x2+x-3;③y=3x2+7x+3.其中函数图象与x轴有两个交点的是
①③
①③
.分析:对各选项二次函数解析式令y=0,利用根的判别式进行判断即可.
解答:解:①令y=0,△=b2-4ac>0,与x轴有2个交点,
②令y=0,△=b2-4ac=1-4×1×3=-16<0,与x轴没有交点,
③令y=0,△=b2-4ac=72-4×3×3=13>0,与x轴有2交点,
故答案为①③.
②令y=0,△=b2-4ac=1-4×1×3=-16<0,与x轴没有交点,
③令y=0,△=b2-4ac=72-4×3×3=13>0,与x轴有2交点,
故答案为①③.
点评:本题考查了抛物线与x轴的交点问题,是基础题,利用根的判别式进行解答即可.

练习册系列答案
相关题目
 (2012•当涂县模拟)如图,给出的二次函数y=ax2+bx+c的图象,对于这个函数有下列五个结论:
(2012•当涂县模拟)如图,给出的二次函数y=ax2+bx+c的图象,对于这个函数有下列五个结论: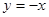 ;②
;② ;③
;③ ;④
;④ 中,二次函数的个数为 ( )
中,二次函数的个数为 ( ) 如图,给出的二次函数y=ax2+bx+c的图象,对于这个函数有下列五个结论:
如图,给出的二次函数y=ax2+bx+c的图象,对于这个函数有下列五个结论: