题目内容
【题目】如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.

(1)求证:AM=AD+MC;
(2)AM=DE+BM是否成立?请直接做出判断,不需要证明.
【答案】
(1)
证明:延长AE、BC交于点N,如图1(1),
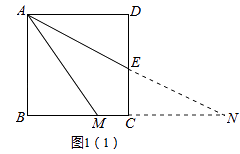
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
在△ADE和△NCE中, 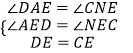 ,
,
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴MA=MN=NC+MC=AD+MC;

(2)
解:AM=DE+BM成立,
理由如下:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
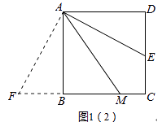
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAB=90°﹣∠BAE=∠DAE,
在△ABF和△ADE中, 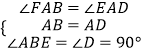 ,
,
∴△ABF≌△ADE(ASA),
∴BF=DE,∠F=∠AED,
∵AB∥DC,
∴∠AED=∠BAE,
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∴AM=FB+BM=DE+BM.

【解析】(1)延长AE、BC交于点N,如图1(1)所示,由四边形ABCD为正方形,得到AD与BC平行,利用两直线平行内错角相等得到一对角相等,再由AE为角平分线得到一对角相等,根据DE=CE,利用AAS得到三角形ADE与三角形NCE全等,利用全等三角形对应边相等得到AD=NC,由MN=MC+CN,等量代换即可得证;(2)AM=DE+BM成立,理由为:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示,由四边形ABCD为正方形,得到四个内角为直角,AB=AD,且AB与DC平行,根据AF与AE垂直,利用等角的余角相等得到一对角相等,利用ASA得到三角形ABF与三角形ADE全等,利用全等三角形对应角相等,对应边相等得到BF=DE,∠F=∠AED,再由AB与DC平行,得到一对内错角相等,等量代换得到一对角相等,利用等角对等边得到AM=FM,等量代换即可得证.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

