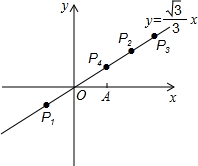
题目内容
在平面直角坐标系中,点A坐标为(1,0),在直线y=
x上取点P,使△OPA是等腰三角形,求所有满足条件的点P坐标.

| ||
| 3 |

如图所示:
①在直线y=
x上作OP=OA,可得符合条件的P1、P2点,
P1坐标为(-
,-
),P2(
,
),
②以A为圆心,1为半径作弧交直线y=
x于点P3,点P3符合条件,P3坐标为(
,
),
③线段OA的垂直平分线交直线y=
x于点P4,点P4符合条件,P4点坐标为(
,
).
故答案为:P1(-
,-
),P2(
,
),P3(
,
),P4(
,
).
①在直线y=
| ||
| 3 |
P1坐标为(-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
②以A为圆心,1为半径作弧交直线y=
| ||
| 3 |
| 3 |
| 2 |
| ||
| 2 |
③线段OA的垂直平分线交直线y=
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
故答案为:P1(-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |


练习册系列答案
相关题目