题目内容
在平面直角坐标系系xOy中，直线y=2x+m与y轴交于点A，与直线y=﹣x+4交于点B（3，n），P为直线y=﹣x+4上一点．
（1）求m，n的值；
（2）当线段AP最短时，求点P的坐标．
（1）m=-5,n=1；（2）P（
，﹣
）
解析试题分析：（1）首先把点B（3，n）代入直线y=﹣x+4得出n的值，再进一步代入直线y=2x+m求得m的值即可；
（2）过点A作直y=﹣x+4的垂线，垂足为P，进一步利用等腰直角三角形的性质和（1）中与y轴交点的坐标特征解决问题．
试题解析：（1）∵点B（3，n）在直线上y=﹣x+4，
∴n=1，
∵点B（3，1）在直线上y=2x+m上，
∴m=﹣5．
（2）过点A作直线y=﹣x+4的垂线，垂足为P，
此时线段AP最短．
∴∠APN=90°，
∵直线y=﹣x+4与y轴交点N（0，4），直线y=2x﹣5与y轴交点A（0，5），
∴AN=9，∠ANP=45°，
∴AM=PM=，
∴OM=
∴P（，﹣）．
考点：1.一次函数图象上点的坐标特征；2.垂线段最短
练习册系列答案
相关题目
的解为 .
反映了某产品的销售收入与销售量之间的关系，
反映了该产品的销售成本与销售量之间的关系。当销售收入大于销售成本时该产品才开始盈利。由图可知，该产品的销售量达到____________ 后，生产该产品才能盈利。
种植草莓大户张华现有22吨草莓等售，现有两种销售渠道：一是运往省城直接批发给零售商；二是在本地市场零售.经过调查分析，这两种销售渠道每天销量及每吨所获纯利润见下表：
| 销售渠道 | 每日销量（吨） | 每吨所获纯利润（元） |
| 省城批发 | ４ | 1200 |
| 本地零售 | １ | 2000 |
受客观因素影响，每天只能采用一种销售渠道，草莓必须在10日内售出．
（1）若一部分草莓运往省城批发给零售商，其余在本地市场零售，请写出销售22吨草莓所获纯利润y（元）与运往省城直接批发给零售商的草莓量x（吨）之间的函数关系式；
（2）由于草莓必须在10日内售完，请你求出x的取值范围；
（3）怎样安排这22吨草莓的销售渠道，才能使所获纯利润最大？并求出最大纯利润．
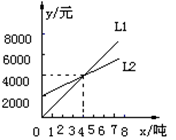
的图象与
轴交于点
，与
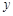轴交于点
． 
，
两点的坐标；
，且使△A
与双曲线
相交于A、B两点，已知点A（﹣2，﹣1）．
和
分别表示某日从上午8点到上午11点，每个普通售票窗口售出的车票数
（张）和每个无人售票窗口售出的车票数
（张）关于售票时间
（小时）的函数图象．