题目内容
探索规律观察下面由※组成的图案和算式，解答问题：
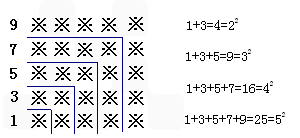
（1）请猜想1+3+5+7+9+…+19= ；
（2）请猜想1+3+5+7+9+…+（2n-1）= ；
（3）请用上述规律计算：103+105+107+…+2003+2005
（2）请猜想1+3+5+7+9+…+（2n-1）= ；
（3）请用上述规律计算：103+105+107+…+2003+2005
解：（1）1+3+5+7+9+…+19=100；
（2）1+3+5+7+9+…+（2n-1）=n2；
（3）103+105+107+…+2003+2005
=（1+3+5+7+9+…+2005）-（1+3+5+7+9+…+101）
=
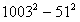
=1003408
（2）1+3+5+7+9+…+（2n-1）=n2；
（3）103+105+107+…+2003+2005
=（1+3+5+7+9+…+2005）-（1+3+5+7+9+…+101）
=
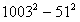
=1003408
练习册系列答案
相关题目
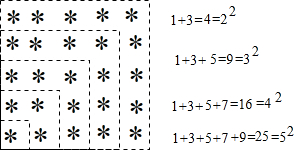探索规律
探索规律观察下面由※组成的图案和算式，解答问题：