题目内容
 如图:牟强老师家有个边长为4米的正方形院子AOBC,他想在院子里建一座的矩形水池DOEF,水池一面DO靠墙AO另一面OE靠OB,若设OD=x(米),OE=y(米).
如图:牟强老师家有个边长为4米的正方形院子AOBC,他想在院子里建一座的矩形水池DOEF,水池一面DO靠墙AO另一面OE靠OB,若设OD=x(米),OE=y(米).
(1)若矩形水池的面积为2平方米,则y与x的函数关系式为:________,在下图中画出能建水池的F点的位置.并用c1标记;
(2)若周长为6米(包含两边靠墙的地方),则y与x的关系式为________,在下图中画出满足条件的水池一角F的所有位置.并用c2标记;
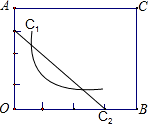
(3)有没有同时满足条件(1)(2)的水池,若有请帮忙找出这一点,在图中画出来,若没有说明理由.
 解:(1)∵矩形水池的面积为2平方米,
解:(1)∵矩形水池的面积为2平方米,∴xy=2,
∴y与x的函数关系式为:y=
 ;
;F点的位置如图.
(2)∵周长为6米,
∴2(x+y)=6,
∴y与x的函数关系式为:y=3-x;
F点的位置如图.C1
(3)令
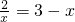 ,
,解得x=1或2,
把x=1或2代入y=3-x,
解得y=2或1,
∴存在点F(1,2)和F(2,1)同时满足(1)(2).
分析:(1)利用矩形的面积计算方法可得xy=2,并由此得到函数关系式;
(2)利用矩形的周长计算方法可得2(x+y)=6,并由此得到函数关系式即可;
(3)联立两个函数若能求得交点坐标则存在,否则就不存在.
点评:本题考查了反比例函数的应用,解题的关键是利用矩形的周长或面积的计算方法得到其函数关系式.

练习册系列答案
相关题目
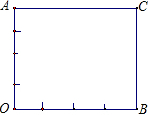 如图:牟强老师家有个边长为4米的正方形院子AOBC,他想在院子里建一座的矩形水池DOEF,水池一面DO靠墙AO另一面OE靠OB,若设OD=x(米),OE=y(米).
如图:牟强老师家有个边长为4米的正方形院子AOBC,他想在院子里建一座的矩形水池DOEF,水池一面DO靠墙AO另一面OE靠OB,若设OD=x(米),OE=y(米).