题目内容
解方程与不等式组:
(1)解方程组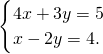
(2)解不等式组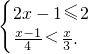 .
.
(1)解: ,
,
∵由②得:x=4+2y③,
把③代入①得:4(4+2y)+3y=5,
解得:y=-1,
把y=-1代入③得:x=4+2×(-1)=2,
∴原方程组的解为: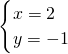 ;
;
(2)解: ,
,
∵解不等式①得:x≤ ,
,
解不等式②得:x>-3,
∴不等式组的解集是:-3<x≤ .
.
分析:(1)由②得出x=4+2y,代入①得出4(4+2y)+3y=5,求出y,把y的值代入x=4+2y求出x,即可得出答案;
(2)根据不等式的性质求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
点评:本题考查了解不等式组和解方程组的应用,解(1)小题的关键是能把方程组转化成解一元一次方程,解(2)小题的关键是能根据不等式的解集找出不等式组的解集.
 ,
,∵由②得:x=4+2y③,
把③代入①得:4(4+2y)+3y=5,
解得:y=-1,
把y=-1代入③得:x=4+2×(-1)=2,
∴原方程组的解为:
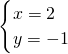 ;
;(2)解:
 ,
,∵解不等式①得:x≤
 ,
,解不等式②得:x>-3,
∴不等式组的解集是:-3<x≤
 .
.分析:(1)由②得出x=4+2y,代入①得出4(4+2y)+3y=5,求出y,把y的值代入x=4+2y求出x,即可得出答案;
(2)根据不等式的性质求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
点评:本题考查了解不等式组和解方程组的应用,解(1)小题的关键是能把方程组转化成解一元一次方程,解(2)小题的关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
 ;
;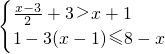 .
. ;
;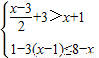 .
.