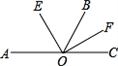
题目内容
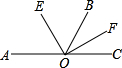如图所示，设相邻两个角∠AOB，∠BOC的平分线分别为OE，OF，且∠EOF是直角，你能说明OA，OC为什么成一条直线吗？试试看吧!
解：∵OE、OF分别平分∠AOB、∠BOC，且∠EOF是直角，
∴∠AOE=∠BOE，∠COF=∠BOF，∠EOF=90°，
∴（∠AOE+∠EOB）+（∠COF+∠BOF）=2×90°=180°，
即∠AOB+∠BOC=180°，
∴∠AOC=180°，
∴AO、OC成一直线（即A，O，C三点共线）．
分析：判断OA，OC是否成一条直线，只要求∠AOC，看是否是180°．
点评：判断A，O，C三点共线的方法就是转化为求∠AOC的度数．
∴∠AOE=∠BOE，∠COF=∠BOF，∠EOF=90°，
∴（∠AOE+∠EOB）+（∠COF+∠BOF）=2×90°=180°，
即∠AOB+∠BOC=180°，
∴∠AOC=180°，
∴AO、OC成一直线（即A，O，C三点共线）．
分析：判断OA，OC是否成一条直线，只要求∠AOC，看是否是180°．
点评：判断A，O，C三点共线的方法就是转化为求∠AOC的度数．
练习册系列答案
相关题目
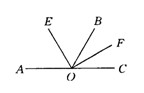24、如图所示，设相邻两个角∠AOB，∠BOC的平分线分别为OE，OF，且∠EOF是直角，你能说明OA，OC为什么成一条直线吗？试试看吧!
