Question

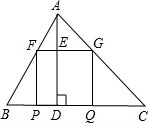（2011•锦江区模拟）如图，AD是△ABC的高，点P，Q在BC边上，点G在AC边上，点F在AB边上，BC=60cm，AD=30cm，四边形PQGF是正方形．
（1）△AFG与△ABC相似的吗？为什么？
（2）FP：BC的值．

Answer 1

分析：（1）由四边形PQGF是正方形，即可得FG∥PQ，由平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，即可证得△AFG与△ABC相似；
（2）首先设PF=FG=PQ=xcm，然后由相似三角形对应高的比等于相似比，即可求得x的值，继而求得FP：BC的值．

解答：解：（1）△AFG∽△ABC．
理由：∵四边形PQGF是正方形，
∴FG∥PQ，即FG∥BC，
∴△AFG∽△ABC；

（2）∵四边形PQGF是正方形，
∴设PF=FG=PQ=xcm，FG∥PQ，
∵AD是△ABC的高，
∴AD⊥BC，AD⊥FG，
∴四边形EFPD是矩形，
∴DE=PF=xcm，
∴AE=AD-DE=30-x（cm），
∵△AFG∽△ABC，
∴

FG

BC

=

AE

AD

，
即

x

60

=

30-x

30

，
解得：x=20，即FP=20cm，
∴FP：BC=20：60=1：3．

点评：此题考查了相似三角形的判定与性质、正方形的性质以及矩形的判定与性质．此题难度适中，解题的关键是掌握数形结合思想与方程思想的应用．