题目内容
已知,如图,直角坐标系中的等腰梯形ABCD,AB∥CD,下底AB在x轴上,D在y轴上,M为AD的中点,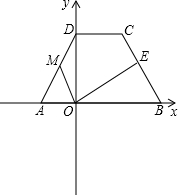 过O作腰BC的垂线交BC于点E.
过O作腰BC的垂线交BC于点E.(1)求证:OM⊥OE;
(2)若等腰梯形中AD所在的直线的解析式为y=
| 4 |
| 3 |
| DC |
| AB |
| 1 |
| 4 |
(3)若点M在梯形ABCD内沿水平方向移动到N,且使四边形MNCD为平行四边形,抛物线上是否存在一点P,使S△PAB与四边形MNCD的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
分析:(1)已知OE⊥BC,则∠OBE+∠BOE=90°,欲求OM⊥OE,即∠MOA+∠BOE=90°,就必须先证得∠MOA=∠OBE,在Rt△OAD中,M是斜边AD的中点,则OM=AM,得∠OAM=∠MOA,而等腰梯形ABCD的两底角∠OAM=∠OBE,通过等量代换即可证得∠MOA=∠OBE,由此得证.
(2)根据直线AD的解析式,可求得点A、D的坐标,即可得到OA、OD的长,已知了DC、AB的比例关系,结合等腰梯形的对称性即可求得AB、CD的长,从而得到C、B的坐标,可根据A、B、D三点的坐标,利用待定系数法求出抛物线的解析式,然后再代入C点坐标进行验证即可.
(3)根据A、D的坐标,易得线段AD中点M的坐标;以DC为底,D、M纵坐标差的绝对值为高,可求得平行四边形MNCD的面积,即可得到△PAB的面积;在△ABP中,底边AB为定长,根据已求得的三角形面积,可得到P点纵坐标的绝对值,将其代入抛物线的解析式中,即可求得点P的坐标,需注意的是P点纵坐标有正、负两种情况,需要分类讨论.
(2)根据直线AD的解析式,可求得点A、D的坐标,即可得到OA、OD的长,已知了DC、AB的比例关系,结合等腰梯形的对称性即可求得AB、CD的长,从而得到C、B的坐标,可根据A、B、D三点的坐标,利用待定系数法求出抛物线的解析式,然后再代入C点坐标进行验证即可.
(3)根据A、D的坐标,易得线段AD中点M的坐标;以DC为底,D、M纵坐标差的绝对值为高,可求得平行四边形MNCD的面积,即可得到△PAB的面积;在△ABP中,底边AB为定长,根据已求得的三角形面积,可得到P点纵坐标的绝对值,将其代入抛物线的解析式中,即可求得点P的坐标,需注意的是P点纵坐标有正、负两种情况,需要分类讨论.
解答:解:(1)∠A=∠B;
因为M为直角三角形AOD的斜边中点,
所以OM=MA,
则∠A=∠MOA,
所以∠MOA=∠B;
又因为OE⊥BC,
所以∠B+∠BOE=90°,
所以∠MOA+∠BOE=90°,则OM⊥OE.
(2)可以求得D(0,4),A(-3,0);
所以OA=3,OD=4,AB=8,DC=2,
所以B(5,0)、C(2,4);
设过A、B、D的抛物线为y=a(x+3)(x-5),
将点D的坐标代入,求出a=-
,
即y=-
(x+3)(x-5),
验证点C也在此抛物线上,所以所求的抛物线为y=-
(x+3)(x-5).
(3)可以求出N(0.5,2),所以平行四边形MNCD的面积为4;
设P(m,n),又AB=8,
所以
|n|×8=4,则|n|=1,所以n=±1;
当n=1时,1=-
(x+3)(x-5),所以x=-
或
;
当n=-1时,-1=-
(x+3)(x-5),所以x=
;
因此这样的点P有四个,分别为(-
,1)、(
,1)、(
,-1)、(
,-1).
因为M为直角三角形AOD的斜边中点,
所以OM=MA,
则∠A=∠MOA,
所以∠MOA=∠B;
又因为OE⊥BC,
所以∠B+∠BOE=90°,
所以∠MOA+∠BOE=90°,则OM⊥OE.
(2)可以求得D(0,4),A(-3,0);
所以OA=3,OD=4,AB=8,DC=2,
所以B(5,0)、C(2,4);
设过A、B、D的抛物线为y=a(x+3)(x-5),
将点D的坐标代入,求出a=-
| 4 |
| 15 |
即y=-
| 4 |
| 15 |
验证点C也在此抛物线上,所以所求的抛物线为y=-
| 4 |
| 15 |
(3)可以求出N(0.5,2),所以平行四边形MNCD的面积为4;
设P(m,n),又AB=8,
所以
| 1 |
| 2 |
当n=1时,1=-
| 4 |
| 15 |
| 5 |
| 2 |
| 9 |
| 2 |
当n=-1时,-1=-
| 4 |
| 15 |
2±
| ||
| 2 |
因此这样的点P有四个,分别为(-
| 5 |
| 2 |
| 9 |
| 2 |
2+
| ||
| 2 |
2-
| ||
| 2 |
点评:此题考查的知识点有:直角三角形、等腰梯形的性质,抛物线解析式的确定,图形面积的求法等.要注意的是(3)题中,根据△ABP的面积求得的点P纵坐标应有正、负两种情况,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目