题目内容
某地区一种商品的需求量y1(万件)、供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-36.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定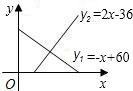 价格,需求量称为稳定需求量.
价格,需求量称为稳定需求量.
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围,该商品的需求量低于供应量;
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
解:(1)当y1=y2时,有-x+60=2x-36.
∴x=32,
此时-x+60=28,
所以该商品的稳定价格为32元/件,稳定需求量为28万件;
(2)因为“需求量为0时,即停止供应”,
∴当y1=0时,有x=60,
又-x+60<2x-36
解得:x>32,
∴当价格大于32元/件而小于60元/件时,该商品的需求量低于供应量;
(3)设政府部门对该商品每件应提供a元补贴.
根据题意,得方程组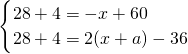
解这个方程组,得 .
.
所以,政府部门对该商品每件应提供6元的补贴.
分析:(1)实质是求函数的交点坐标,利用y1=y2可求解;
(2)因为“需求量为0时,即停止供应”,所以,当y1=0时,有x=60.又由图象,知x>32,利用题意和图象综合可知当价格大于32元/件而小于60元/件时,该商品的需求量低于供应量;
(3)根据题意列方程组求解即可.
点评:此题主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.
∴x=32,
此时-x+60=28,
所以该商品的稳定价格为32元/件,稳定需求量为28万件;
(2)因为“需求量为0时,即停止供应”,
∴当y1=0时,有x=60,
又-x+60<2x-36
解得:x>32,
∴当价格大于32元/件而小于60元/件时,该商品的需求量低于供应量;
(3)设政府部门对该商品每件应提供a元补贴.
根据题意,得方程组
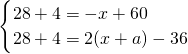
解这个方程组,得
 .
.所以,政府部门对该商品每件应提供6元的补贴.
分析:(1)实质是求函数的交点坐标,利用y1=y2可求解;
(2)因为“需求量为0时,即停止供应”,所以,当y1=0时,有x=60.又由图象,知x>32,利用题意和图象综合可知当价格大于32元/件而小于60元/件时,该商品的需求量低于供应量;
(3)根据题意列方程组求解即可.
点评:此题主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
9、下表是某一地区在一年中不同季节对同一商品的需求情况的统计表(单位:件),如果你是工商局的统计员,要为厂家提供关于这种商品的直观统计图,则应选择的统计图为( )
|
12、下表是某一地区在一年中不同季节对同一商品的需求情况统计(单位:吨):
|
下表是某一地区在一年中不同季节对同一商品的需求情况的统计表(单位:件),如果你是工商局的统计员,要为厂家提供关于这种商品的直观统计图,则应选择的统计图为( )
|
季 度 |
第一季度 |
第二季度 |
第三季度 |
第四季度 |
|
某商品需求量 |
3300 |
1500 |
2700 |
4000 |
A.条形统计图 B.折线统计图 C.扇形统计图 D.前面三种都可以