��Ŀ����
����Ŀ����ͼ����OΪƽ��ֱ������ϵ��ԭ�㣬�ڳ�����OABC�У�OC��AB��OA��BC������OC��OA�ֱ���x���y���ϣ��ҵ�B��a��b�����㣺![]() +��2b+6��2=0��
+��2b+6��2=0��
��1�����B�����ꣻ
��2����ͼ1��������B��ֱ��BP�볤����OABC�ı߽��ڵ�P���ҽ�������OABC�������Ϊ1��3�����֣����P�����ꣻ
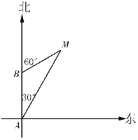
��3����ͼ2��MΪ�߶�OCһ�㣬����ABM=��AMB��N��x�Ḻ������һ���㣬��MAN��ƽ����AD��BM���ӳ����ڵ�D���ڵ�N�˶��Ĺ����У����ж���ANM����D��������ϵ����˵�����ɣ�

���𰸡���1��B��4����3����2����2��0����0����![]() ����3����ANM=2��D
����3����ANM=2��D
��������
��1�����÷Ǹ��������ʼ��ɽ�����⣻
��2�����������ηֱ�������⼴�ɣ�
��3�����ۣ���ANM=2��D����ME��AD��AB��E���ӳ�BA��F������ƽ���ߵ����ʣ���ƽ���ߵĶ��弴�ɽ�����⣻
��1�������⣺4��a=0��2b+6=0��
��a=4��b=��3��
��B��4����3����
��2��������P��OC��ʱ�������⣺S��BCP��S�ı���OABC=1��4��
��![]() CP3=
CP3=![]() ��3��4��
��3��4��
��PC=2��
��OP=4��2=2��
��P��2��0����
������P��OA��ʱ��S��ABP=![]() S�ı���OABC��
S�ı���OABC��
��![]() PA4=
PA4=![]() ��3��4
��3��4
��PA=![]() ��
��
��OP=3��![]() =
=![]() ��
��
��P��0����![]() ����
����
�������������������ĵ�P����Ϊ��2��0����0����![]() ����
����
��3�����ۣ���ANM=2��D��
���ɣ���ME��AD��AB��E���ӳ�BA��F��
��ME��AD��
���1=��D����2=��3��
��ADƽ����MAN��
���MAN=2��3��
��OC��AB��
���ABM=��CMB��
�ߡ�AMB=��CMB��
���AMC=2��AMB��
��OC��AB��
���FAM=��AMC=2��AMB��
���ANM=2��AMB��2��3
=2��AMB��2��2
=2����AMB����2��
=2��1
=2��D��

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�