题目内容
 (2012•石家庄二模)如图1,直径AC、BD将圆O四等分,动点P从圆心O出发,沿O→C→D→O路线作匀速运动,若圆O的半径为1,设运动x时间为x(s),∠APB=y°,y与x之间的函数关系如图2所示,则点M的横坐标应为( )
(2012•石家庄二模)如图1,直径AC、BD将圆O四等分,动点P从圆心O出发,沿O→C→D→O路线作匀速运动,若圆O的半径为1,设运动x时间为x(s),∠APB=y°,y与x之间的函数关系如图2所示,则点M的横坐标应为( )分析:通过函数图象可以得到函数随自变量的变化规律,通过规律结合图象可以求出关键点C、D的坐标值,从而求出M的横坐标.
解答:解:根据题意,可知点P从圆心O出发,运动到点C时,∠APB的度数由90°减小到45°,
∵在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为
π,
由图象2可得:M的横坐标是∠APB由稳定在45°保持不变到增大的转折点;
故可得M的横坐标所对应的点是D点,表示这时P点运动到了D点.
从而可得M横=OC+弧CD的长=
π+1.
故选C.
∵在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为
| 1 |
| 2 |
由图象2可得:M的横坐标是∠APB由稳定在45°保持不变到增大的转折点;
故可得M的横坐标所对应的点是D点,表示这时P点运动到了D点.
从而可得M横=OC+弧CD的长=
| 1 |
| 2 |
故选C.
点评:本题是一道动点问题的函数图象试题,考查了函数图象横、纵坐标表示的意义,让学生对分段函数有一个认识和理解的过程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
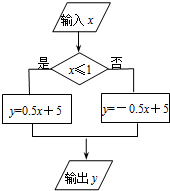 (2012•石家庄二模)如图,根据流程图中的程序,当输出数值y为1时,输入数值x为( )
(2012•石家庄二模)如图,根据流程图中的程序,当输出数值y为1时,输入数值x为( ) (2012•石家庄二模)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
(2012•石家庄二模)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )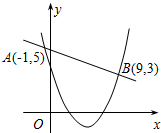 (2012•石家庄二模)如图,一次函数y1=mx+n(m≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于两点A(-1,5)、B(9,3),请你根据图象写出使y1≥y2成立的x的取值范围( )
(2012•石家庄二模)如图,一次函数y1=mx+n(m≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于两点A(-1,5)、B(9,3),请你根据图象写出使y1≥y2成立的x的取值范围( )