题目内容
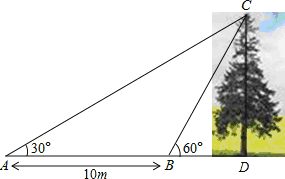
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度.
【答案】这棵树的高度为5![]() 米.
米.
【解析】
试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=60°,∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD-∠A=60°-30°=30°,
∵∠A=30°,
∴∠A=∠ACB,
∵AB=10,
∴BC=AB=10,
在R△BCD中,CD=BCsin∠CBD=10×![]() =5
=5![]() .
.
答:这棵树的高度为5![]() 米.
米.

练习册系列答案
相关题目
【题目】小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
天数 | 3 | 7 | 5 | 12 | 3 |
在每天所走的步数这组数据中,中位数是______(万步).
【题目】在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0).现以原点为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为_______.
【题目】某校篮球班21名同学的身高如下表
身高cm | 180 | 186 | 188 | 192 | 208 |
人数(个) | 4 | 6 | 5 | 4 | 2 |
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A. 186,186 B. 186,187 C. 186,188 D. 208,188