题目内容
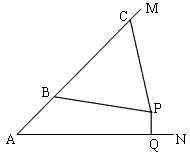
 如图,汶川地震后,某处废墟堆成的斜坡AM的坡度为1:1.生命探测仪显示P处有生命迹象,估计距离斜坡上的B、C处均为5米.已知水平线AN、直线AM与点P都在同一平面上,且AB=3米,BC=6米.过点P作PQ⊥AN,垂足为Q,试确定AQ和PQ的长度.
如图,汶川地震后,某处废墟堆成的斜坡AM的坡度为1:1.生命探测仪显示P处有生命迹象,估计距离斜坡上的B、C处均为5米.已知水平线AN、直线AM与点P都在同一平面上,且AB=3米,BC=6米.过点P作PQ⊥AN,垂足为Q,试确定AQ和PQ的长度.
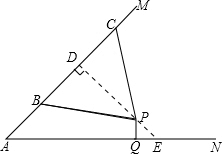 解:作PD⊥AM于D,延长DP交AN于E.
解:作PD⊥AM于D,延长DP交AN于E.∵BP=CP,BC=6米.
∴BD=CD=3米.
∵BP=5米.
∴由勾股定理得PD=4米,
由AM坡度1:1得∠A=45°.
∵∠ADE=90°.
∴△ADE为等腰直角三角形.
∵AD=AB+BD=6米.
由勾股定理得AE=6
 米.
米.∵DE=AD=6米,PD=4米.
∴PE=2米.
∵△QPE中∠PQE=90°,∠E=45°.
∴△PQE为等腰直角三角形.
由勾股定理得PQ=QE=
 米.
米.∴AQ=AE-QE=5
 米,
米,∴AQ=5
 米,PQ=
米,PQ= 米.
米.分析:根据PC=BP,做等腰三角形底边上的高,得到等腰直角三角形△PQE和△ADE,利用勾股定理即可求得相应的线段的长度.
点评:本题通过构造等腰直角三角形,利用等腰直角三角形的性质和勾股定理求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
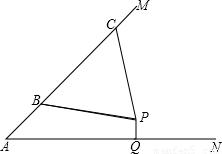
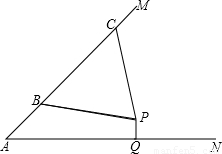
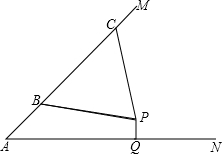
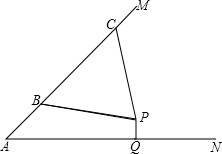 如图,汶川地震后,某处废墟堆成的斜坡AM的坡度为1:1.生命探测仪显示P处有生命迹象,估计距离斜坡上的B、C处均为5米.已知水平线AN、直线AM与点P都在同一平面上,且AB=3米,BC=6米.过点P作PQ⊥AN,垂足为Q,试确定AQ和PQ的长度.
如图,汶川地震后,某处废墟堆成的斜坡AM的坡度为1:1.生命探测仪显示P处有生命迹象,估计距离斜坡上的B、C处均为5米.已知水平线AN、直线AM与点P都在同一平面上,且AB=3米,BC=6米.过点P作PQ⊥AN,垂足为Q,试确定AQ和PQ的长度.