题目内容
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
| A.7:20 | B.7:30 | C.7:45 | D.7:50 |
A.
解析试题分析:∵开机加热时每分钟上升10℃,∴从30℃到100℃需要7分钟.
设一次函数关系式为:y=k1x+b,将(0,30),(7,100)代入y=k1x+b得k1=10,b=30. ∴y=10x+30(0≤x≤7).
令y=50,解得x=2.
设反比例函数关系式为: ,将(7,100)代入
,将(7,100)代入 得k=700,∴
得k=700,∴ 。
。
将y=30代入 ,解得
,解得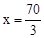 ,∴
,∴ (7≤x≤
(7≤x≤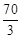 ).
).
令y=50,解得x=14.
∴饮水机的一个循环周期为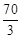 分钟.每一个循环周期内,在0≤x≤2及14≤x≤
分钟.每一个循环周期内,在0≤x≤2及14≤x≤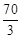 时间段内,水温不超过50℃.
时间段内,水温不超过50℃.
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85﹣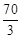 ×3=15,位于14≤x≤
×3=15,位于14≤x≤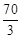 时间段内,故可行;
时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75﹣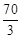 ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤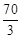 时间段内,故不可行;
时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60﹣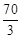 ×2=
×2=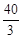 ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤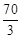 时间段内,故不可行;
时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55﹣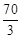 ×2=
×2=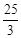 ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤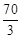 时间段内,故不可行.
时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意. 故选A.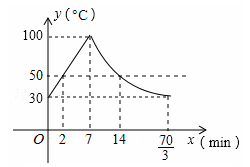
考点:1.一次函数和反比例函数的应用;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.分类思想的应用.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案已知一次函数y=kx+b的图象经过第一、二、三象限,则b的值可以是 ( )
| A.﹣2 | B.-1 | C.0 | D.2 |
从3,4,5这三个数中任取两个,分别记作p和q(p≠q),构造函数y=px-2和y=x+q,使这两个函数图象交点的横坐标始终小于2,则这样的有序数组(p,q)共有( ).
| A.2对 | B.3对 | C.4对 | D.5对 |
若一次函数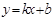 ,当
,当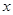 的值减小1,
的值减小1,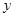 的值就减小2,则当
的值就减小2,则当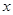 的值增加2时,
的值增加2时,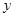 的值( )
的值( )
| A.减小2 | B.增加2 | C.减小 4 | D.增加4 |
函数y=3x﹣4与函数y=2x+3的交点的坐标是( )
| A.(5,6) | B.(7,﹣7) | C.(﹣7,﹣17) | D.(7,17) |
对于点A(x1,y1),B(x2,y2),定义一种运算: .例如,A(-5,4),B(2,﹣3),
.例如,A(-5,4),B(2,﹣3), .若互不重合的四点C,D,E,F,满足
.若互不重合的四点C,D,E,F,满足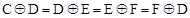 ,则C,D,E,F四点【 】
,则C,D,E,F四点【 】
| A.在同一条直线上&nbs, | B.在同一条抛物线上&nbs, |
| C.在同一反比例函数图象上&nbs, | D.是同一个正方形的四个顶点&nbs, |




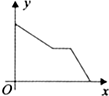
 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )