题目内容
 (2010•广阳区二模)如图,抛物线y=-x2+2nx+n2-9(n为常数)经过坐标原点和x轴上的另一点C,顶点在第一象限.
(2010•广阳区二模)如图,抛物线y=-x2+2nx+n2-9(n为常数)经过坐标原点和x轴上的另一点C,顶点在第一象限.(1)确定该抛物线的解析式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P在该函数图象上,且点P到x轴的距离为8,求出点P的坐标.
分析:(1)将原点代入解析式,可求出n的值,根据顶点坐标在第一象限,可得出n的值,即可得抛物线的解析式;
(2)根据抛物线的对称轴x=-
,即可求出;然后,把x的值代入解析式即可求出顶点的纵坐标;
(3)设点P的坐标为:(x,8)或(x,-8),代入解析式,求出x的值,即可解答;
(2)根据抛物线的对称轴x=-
| b |
| 2a |
(3)设点P的坐标为:(x,8)或(x,-8),代入解析式,求出x的值,即可解答;
解答:解:(1)∵抛物线y=-x2+2nx+n2-9(n为常数)经过坐标原点,
∴可得,0=n2-9,解得n=±3,
又∵顶点在第一象限,
即x=-
>0,得n>0,
∴n=3,
∴该抛物线的解析式为:y=-x2+6x;
(2)抛物线的对称轴为:x=-
=3,
∴y=-9+18=9,
∴抛物线的顶点坐标为:(3,9);
(3)根据题意,
设点P的坐标为:(x,8)或(x,-8),
∴8=-x2+6x或-8=-x2+6x,
整理得x2-6x+8=0或x2-6x-8=0,
解得x=2或x=4;x=3±
;
∴点P的坐标为:(2,8)或(4,8)或(3-
,-8)或(3+
,-8).

∴可得,0=n2-9,解得n=±3,
又∵顶点在第一象限,
即x=-
| 2n |
| 2×(-1) |
∴n=3,
∴该抛物线的解析式为:y=-x2+6x;
(2)抛物线的对称轴为:x=-
| 2×3 |
| 2×(-1) |
∴y=-9+18=9,
∴抛物线的顶点坐标为:(3,9);
(3)根据题意,
设点P的坐标为:(x,8)或(x,-8),
∴8=-x2+6x或-8=-x2+6x,
整理得x2-6x+8=0或x2-6x-8=0,
解得x=2或x=4;x=3±
| 17 |
∴点P的坐标为:(2,8)或(4,8)或(3-
| 17 |
| 17 |
点评:本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养,要会利用数形结合的思想把代数和几何图形结合起来.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
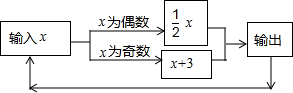 出的结果为24,第2次输出的结果为12,…第2010次输出的结果为( )
出的结果为24,第2次输出的结果为12,…第2010次输出的结果为( )
 点Q也随之停止运动.
点Q也随之停止运动.