题目内容
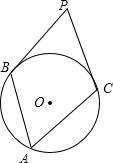（2012•连云港）如图，圆周角∠BAC=55°，分别过B，C两点作⊙O的切线，两切线相交于点P，则∠BPC=70
70
°．分析：首先连接OB，OC，由PB，PC是⊙O的切线，利用切线的性质，即可求得∠PBO=∠PCO=90°，又由圆周角定理可得：∠BOC=2∠BAC，继而求得∠BPC的度数．
解答：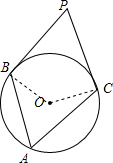
解：连接OB，OC，
∵PB，PC是⊙O的切线，
∴OB⊥PB，OC⊥PC，
∴∠PBO=∠PCO=90°，
∵∠BOC=2∠BAC=2×55°=110°，
∴∠BPC=360°-∠PBO-∠BOC-∠PCO=360°-90°-110°-90°=70°．
故答案为：70．
解：连接OB，OC，∵PB，PC是⊙O的切线，
∴OB⊥PB，OC⊥PC，
∴∠PBO=∠PCO=90°，
∵∠BOC=2∠BAC=2×55°=110°，
∴∠BPC=360°-∠PBO-∠BOC-∠PCO=360°-90°-110°-90°=70°．
故答案为：70．
点评：此题考查了切线的性质、圆周角定理以及四边形的内角和定理．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
沿AO方向、乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．