Question

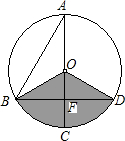如图，已知在⊙O中，AB=4

3

，AC是⊙O的直径，AC⊥BD于F，∠A=30°．
（1）求图中阴影部分的面积；
（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．
（3）试判断⊙O中其余部分能否给（2）中的圆锥做两个底面．

Answer 1

分析：（1）由∠A=30°，可求得∠BOC=60°，再根据垂径定理得∠BOD=120°，由勾股定理得出BF以及OB的长，从而计算出阴影部分的面积即扇形的面积．
（2）设出底面半径，利用扇形的面积和圆弧的关系求解即可；
（3）上题求得的半径与AO比较后即可得到答案．

解答：解：（1）∵AC⊥BD于F，∠A=30°，
∴∠BOC=60°，∠OBF=30°，
∵在Rt△ABF中，AB=4

3

，
∴BF=2

3

，
∴OB=BF÷cos30°=2

3

÷

3

2

=4，
∴S_阴影=S_扇形BOD=

120•π•42

360

=

16

3

π；

（2）设底面半径为r，
∵半径OB=4，
∴4πr=

16

3

π
∴r=

4

3

；

（3）∵OB=4＞

4

3

，
∴⊙O中其余部分能给（2）中的圆锥做两个底面．

点评：本题考查了扇形面积的计算，以及圆周角定理、垂径定理和勾股定理，是基础知识要熟练掌握．