题目内容
 阅读框图并回答下列问题:
阅读框图并回答下列问题:(1)若A为785,则E=
1089
1089
;(2)按框图流程,取不同的三位数A,所得E的值都相同吗?如果相同,请说明理由;如果不同,请求出E的所有可能的值;
(3)将框图中的第一步变为“任意写一个个位数字不为0的三位数1,它的百位数字减去个位数字所得的差大于2”.其余的步骤不变,请猜想E的值并对你猜想的结论加以证明.
分析:(1)由A=785,根据框图中的流程计算即可得到E;
(2)E的值相同,理由为:设A=100a+10b+c,且a-c=2,表示出B,求出A-B,得到C,进而求出D,最后求出E即可;
(3)E=1089,理由为:设A=100a+10b+c且a-c>2,表示出B,进而得出C与D,求出E即可.
(2)E的值相同,理由为:设A=100a+10b+c,且a-c=2,表示出B,求出A-B,得到C,进而求出D,最后求出E即可;
(3)E=1089,理由为:设A=100a+10b+c且a-c>2,表示出B,进而得出C与D,求出E即可.
解答:解:(1)由A=785,得到B=587,
∴C=A-B=785-587=198,D=891,
则E=198+891=1089.
(2)E的值都相同,
理由如下:设A=100a+10b+c且a-c=2,则B=100c+10b+a,
∴C=A-B=(100a+10b+c)-(100c+10b+a)=99a-99c=99(a-c)=99×2=198,
∴D=891,
∴E=C+D=198+891=1089.
(3)E=1089,理由为:
设A=100a+10b+c且a-c>2,则B=100c+10b+a,
∴C=A-B=(100a+10b+c)-(100c+10b+a)=100(a-c)-(c-a)=100(a-c-1)+10×9+(10+c-a),
∴D=100(10+c-a)+10×9+(a-c-1),
∴E=C+D=[100(a-c-1)+10×9+(10+c-a)]+[100(10+c-a)+10×9+(a-c-1)]=1089.
∴C=A-B=785-587=198,D=891,
则E=198+891=1089.
(2)E的值都相同,
理由如下:设A=100a+10b+c且a-c=2,则B=100c+10b+a,
∴C=A-B=(100a+10b+c)-(100c+10b+a)=99a-99c=99(a-c)=99×2=198,
∴D=891,
∴E=C+D=198+891=1089.
(3)E=1089,理由为:
设A=100a+10b+c且a-c>2,则B=100c+10b+a,
∴C=A-B=(100a+10b+c)-(100c+10b+a)=100(a-c)-(c-a)=100(a-c-1)+10×9+(10+c-a),
∴D=100(10+c-a)+10×9+(a-c-1),
∴E=C+D=[100(a-c-1)+10×9+(10+c-a)]+[100(10+c-a)+10×9+(a-c-1)]=1089.
点评:此题考查了整式加减的应用,弄清题意是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 似比(a:b).
似比(a:b). 常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.
常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.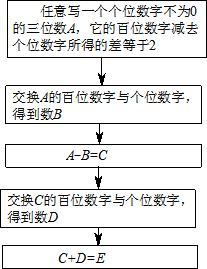 阅读框图并回答下列问题:
阅读框图并回答下列问题: