题目内容
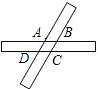
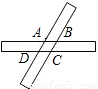
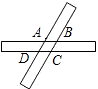 如图,两张宽度相等的长方形纸条交叉重叠在一起,交点分别为A、B、C、D,则四边形ABCD的形状是
如图,两张宽度相等的长方形纸条交叉重叠在一起,交点分别为A、B、C、D,则四边形ABCD的形状是
- A.菱形
- B.矩形
- C.正方形
- D.一般平行四边形
A
分析:先根据长方形的两组对边分别平行,得出AB∥CD,BC∥AD,证出四边形ABCD为平行四边形;再作?ABCD的两条高AE、AF,由两张长方形纸条的宽度相等,得出AE=AF,根据平行四边形的面积不变,证出?ABCD有一组邻边相等;从而根据定义得出
四边形ABCD为菱形.
解答: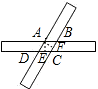 解:∵两张纸条都是长方形,
解:∵两张纸条都是长方形,
∴AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
过点A作AE⊥DC于E,AF⊥BC于F.
∵两张长方形纸条的宽度相等,
∴AE=AF.
又∵?ABCD的面积=DC•AE=BC•AF,
∴DC=BC,
∴?ABCD为菱形.
故选A.
点评:本题主要考查学生对菱形判别方法的掌握;
一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.
分析:先根据长方形的两组对边分别平行,得出AB∥CD,BC∥AD,证出四边形ABCD为平行四边形;再作?ABCD的两条高AE、AF,由两张长方形纸条的宽度相等,得出AE=AF,根据平行四边形的面积不变,证出?ABCD有一组邻边相等;从而根据定义得出
四边形ABCD为菱形.
解答:
 解:∵两张纸条都是长方形,
解:∵两张纸条都是长方形,∴AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
过点A作AE⊥DC于E,AF⊥BC于F.
∵两张长方形纸条的宽度相等,
∴AE=AF.
又∵?ABCD的面积=DC•AE=BC•AF,
∴DC=BC,
∴?ABCD为菱形.
故选A.
点评:本题主要考查学生对菱形判别方法的掌握;
一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.

练习册系列答案
相关题目
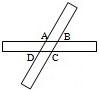 13、如图,两张宽度相等的长方形纸条交叉重叠在一起,交点分别为A、B、C、D,则四边形ABCD的形状是( )
13、如图,两张宽度相等的长方形纸条交叉重叠在一起,交点分别为A、B、C、D,则四边形ABCD的形状是( )