题目内容
(1)已知角a和线段c如图所示,求作等腰三角形ABC,使其底角∠B=a,腰长AB=c,要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
(2)若a=45°,c=2,求此三角形ABC的面积.

分析:(1)可先作出2∠α的补角,即为等腰三角形的顶角,进而作出腰,在腰的同侧作出顶角,在顶角的另一边截取腰长,连接BC即可;
(2)易得此三角形为等腰直角三角形,腰长为2,利用面积公式可得三角形的面积.
(2)易得此三角形为等腰直角三角形,腰长为2,利用面积公式可得三角形的面积.
解答:解:(1)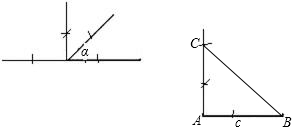 ;
;
(2)∵a=45°,c=2,
∴∠C=∠B=45°,
∴∠A=90°,
∴三角形ABC的面积为
×2×2=2.
 ;
;(2)∵a=45°,c=2,
∴∠C=∠B=45°,
∴∠A=90°,
∴三角形ABC的面积为
| 1 |
| 2 |
点评:考查等腰三角形的画法及面积的计算;得到顶角及度数是解决本题的关键.

练习册系列答案
相关题目
 ,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹。(不写作法)
,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹。(不写作法)
 ,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
 ,使其底角∠B=a,腰长AB
= c, 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
,使其底角∠B=a,腰长AB
= c, 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)

