��Ŀ����
������ȫ�ȵ�ֱ�����ǰ�ABC��EFG������һ��ʹ���ǰ�EFG��ֱ�Ƕ���G�����ǰ�ABC��б���е�O�غϣ����С�B=��F=30�㣬б��AB��EF����Ϊ4����1����EG��AC�ڵ�K��GF��BC�ڵ�Hʱ����ͼ�٣�����GH��GK��ֵ��
��2���ֽ����ǰ�EFG��ͼ����ʾ��λ����O������ʱ�뷽����ת����ת�Ǧ�����������0�㣼����30�㣨��ͼ�ڣ���EG��AC�ڵ�K��GF��BC�ڵ�H��GH��GK��ֵ�Ƿ�ı䣿֤���㷢�ֵĽ��ۣ�
��3���ڢ��£�����HK����������ת�����У���GH=x����GKH�����Ϊy����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��4�����ǰ�EFG��ͼ����ʾ��λ����O����ʱ����תʱ��0�㣼����90�㣬�Ƿ����
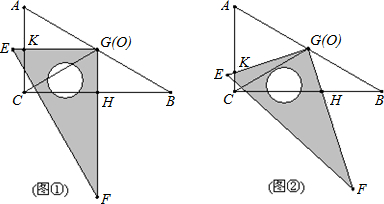 ijλ��ʹ��BFG�ǵ��������Σ������ڣ���ֱ��д����Ӧ����ת�Ǧ����������ڣ�˵�����ɣ�
ijλ��ʹ��BFG�ǵ��������Σ������ڣ���ֱ��д����Ӧ����ת�Ǧ����������ڣ�˵�����ɣ�
��������1������30���ֱ�������ε����߹�ϵ��������֪�������ɶ����������ֱ�������ε����߳��ȣ����������ε���λ�߿������GK����GH��ֵ������������ֵ��
��2����GM��AC��M��GN��BC��N���������������ƿ������GH��GK�ı�ֵ���䣮
��3����GKH��ֱ�������Σ���ֱ�DZߵı�֪��������GKҲ��x��ʽ�ӱ�ʾ���������ֱ�����������ε������ʽ�Ϳ�����������Ľ���ʽ��
��4������ʱ����ת30���90��ʱ����ͼ�Ϳ���֤����EGH�ա�FBH���õ���GEK=��GFB���Ӷ��õ���FGB=��GFB���õ�����ȣ��ó����ۣ���ת90��ʱ Ҳ�ǵó���BGF=��F�����õ����ۣ�
��2����GM��AC��M��GN��BC��N���������������ƿ������GH��GK�ı�ֵ���䣮
��3����GKH��ֱ�������Σ���ֱ�DZߵı�֪��������GKҲ��x��ʽ�ӱ�ʾ���������ֱ�����������ε������ʽ�Ϳ�����������Ľ���ʽ��
��4������ʱ����ת30���90��ʱ����ͼ�Ϳ���֤����EGH�ա�FBH���õ���GEK=��GFB���Ӷ��õ���FGB=��GFB���õ�����ȣ��ó����ۣ���ת90��ʱ Ҳ�ǵó���BGF=��F�����õ����ۣ�
����⣺��1���ߡ�ACB=��EGF=90�㣬��B=��F=30��
��AC=
AB��EG=
EF
��AB=EF=4
��AC=EG=2����Rt��ACB��Rt��EGF�У��ɹ��ɶ�����
BC=GF=2
��GE��AC��GF��BC
��GE��BC��GF��AC
��G��AB���е�
��K��H�ֱ���AC��CB���е�
��GK��GH�ǡ�ABC����λ��
��GK=
BC=
GH=
AC=1
��GH��GK=1��
��2�����䣬
�������£���GM��AC��M��GN��BC��N��
���GMC=��GNH=90������ת�����ʿ�֪��
��2=��1
���GMK�ס�GNH
��
=
��GN��GM=1��
��GH��GK=1��
����ת�Ǧ�����������0�㣼����30��ʱ��GH��GK��ֵ��ֵ���䣮
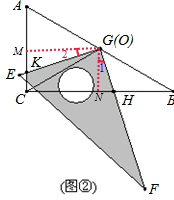
��3������KH���ߡ�EGH=90��
��S��KGH=
��GH=x����GH��GK=1��
��x��GK=1��
��GK=
x
��y=
y=
x2��1��x��
����
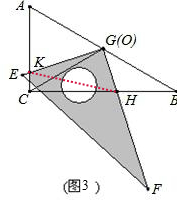
��4�����ڣ�����ͼ������=30����=90��ʱ����BFG�ǵ��������Σ�
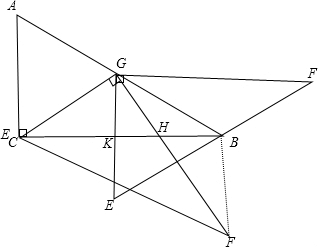
��AC=
| 1 |
| 2 |
| 1 |
| 2 |
��AB=EF=4
��AC=EG=2����Rt��ACB��Rt��EGF�У��ɹ��ɶ�����
BC=GF=2
| 3 |
��GE��AC��GF��BC
��GE��BC��GF��AC
��G��AB���е�
��K��H�ֱ���AC��CB���е�
��GK��GH�ǡ�ABC����λ��
��GK=
| 1 |
| 2 |
| 3 |
GH=
| 1 |
| 2 |
��GH��GK=1��
| 3 |
��2�����䣬
�������£���GM��AC��M��GN��BC��N��
���GMC=��GNH=90������ת�����ʿ�֪��
��2=��1
���GMK�ס�GNH
��
| GH |
| GK |
| GN |
| GM |
��GN��GM=1��
| 3 |
��GH��GK=1��
| 3 |
����ת�Ǧ�����������0�㣼����30��ʱ��GH��GK��ֵ��ֵ���䣮

��3������KH���ߡ�EGH=90��
��S��KGH=
| GH•GK |
| 2 |
��GH=x����GH��GK=1��
| 3 |
��x��GK=1��
| 3 |
��GK=
| 3 |
��y=
x•
| ||
| 2 |
y=
| ||
| 2 |
2
| ||
| 3 |

��4�����ڣ�����ͼ������=30����=90��ʱ����BFG�ǵ��������Σ�

���������⿼�������������ε��ж������ʣ����������ε����ʣ���ת�������Լ����ɶ��������ã�

��ϰ��ϵ�д�
 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
�����Ŀ

 ����������:
����������:


 ����������:
����������:
