题目内容
如图，边长为
的正方形
的中心为
，
中，
，且绕点旋转时，能依次覆盖正方形各顶点（即各顶点在内）。
（1）当
为多少度时，
覆盖的正方形部分的面积始终为正方形面积的
？并说明理由；
（2）求满足（1）的的面积的最小值；
（3）若将条件中正方形换成正
边形，其他条件不变，那么为多少度时，覆盖的正边形的面积始终为正边形的
？这样的的面积最小值为多少？（要求：只写出结果，不写解答过程）
解（1）当
时，
覆盖的正方形部分的面积始终为正方形面积的
当
与对角线共线时，显然成立。
当与正方形对角线不共线时，不妨设
交正方形边于点
，点
（如图）。
，∴
。
又
，
∴
。∴
。
（2）当
点到
的距离等于
长时，
面积最小。
，∴ 
。∴的最小值=
。
（3）符合条件的
。
的最小值=
练习册系列答案
中考解读考点精练系列答案
相关题目
的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形，若拼成的矩形一边长
为4，则另一边长为 
的正方形纸片剪出一个边长为
的正方形之后，剩余部分又剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是（ ）
B．
D．
的正方形纸片剪出一个边长为
的正方形之后，剩余部分又剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是（ ）
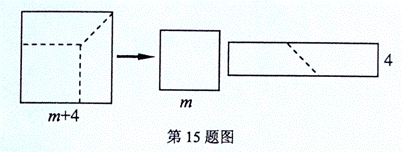
的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形，若拼成的矩形一边长为4，则另一边长为
的正方形纸片剪出一个边长为
的正方形之后，剩余部分可剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是
C．
D．