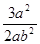题目内容
设绝对值小于1的全体实数的集合为S，在S中定义一种运算“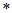
”，
使得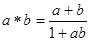
小题1:证明：结合律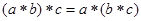
成立
小题2:证明：如果a与b在S中，那么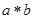
也在S中（说明：可能用到的知识: 
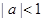即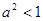
）
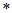”，使得
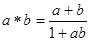
小题1:证明：结合律
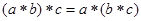成立小题2:证明：如果a与b在S中，那么
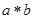也在S中（说明：可能用到的知识: 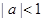即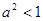）小题1:见解析
小题2:见解析
（1）（
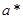b)*c=
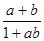*c=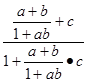
=
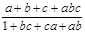因为此式关于a,b,c对称，所以即得(a*b)*c=a*(b*c)成立，这样就利用对称性减少了一半计算
（2）当-1<a<1,-1<b<1时，有-1<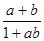<1成立，也即证
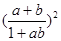<1成立，从而用比较法即可证得
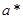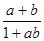b)*c=*c=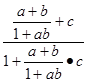=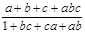因为此式关于a,b,c对称，所以即得(a*b)*c=a*(b*c)成立，这样就利用对称性减少了一半计算（2）当-1<a<1,-1<b<1时，有-1<
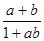<1成立，也即证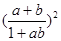<1成立，从而用比较法即可证得
练习册系列答案
阅读快车系列答案
相关题目
；
；
；
；
中，属于分式的有…………………… （ ）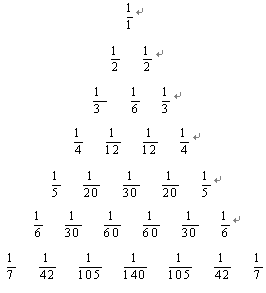 
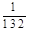
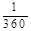
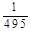
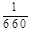
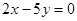,则x:y = .
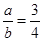，则
( )
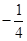
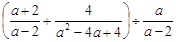
其中m＝3
. 
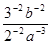化成不含负指数的形式是（ ）
