Question

【题目】已知长方形纸片，点在边上，点在边上，将沿翻折到，射线与交于点.点在边上，将沿翻折到，射线与交于点.

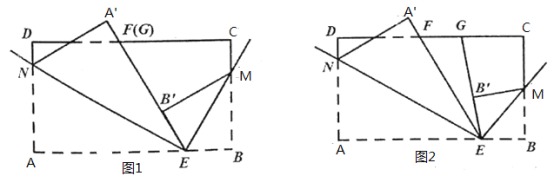
（1）如图1，若点与点重合，直接写出以为顶点的两对相等的角，并求的度数；

（2）如图2，若点在点的右侧，且，，求与的度数；

（3）若点在点的左侧，且，求的度数（用含的代数式表示）.

Answer 1

【答案】（1）∠AEN=∠NEF，∠BEM=∠FEM；∠MEN=90°；（2）∠FEG=24°，∠MEN=102°；（3）∠MEN=90°-α．

【解析】

（1）根据折叠的性质，平角的定义，角的和差定义计算即可；
（2）根据折叠的性质以及平角的定义，可得出∠AEN +∠BEM=（180°-∠FEG），再结合所给的两个等式可得出∠FEG的度数；根据∠MEN=180°-（∠AEN+∠BEM），求出∠AEN+∠BEM即可解决问题；
（3）先画出图形，根据（2）中的思路即可分析出∠MEN与∠FEG之间的等量关系，即可得出结果．

解：（1）根据折叠的性质可得，

以E为顶点的两对相等的角分别为： ∠AEN=∠NEF，∠BEM=∠FEM．
∴∠NEF=∠AEF，∠MEF=∠BEF，
∴∠MEN=∠NEF+∠MEF=∠AEF+∠BEF=（∠AEF+∠BEF）=∠AEB，
∵∠AEB=180°，
∴∠MEN=×180°=90°；

（2）由（1）可得∠AEN=∠AEF，∠BEM=∠BEG，
∴∠AEN +∠BEM =∠AEF+∠BEG=（∠AEF+∠BEG）=（∠AEB-∠FEG）．

∴∠AEN +∠BEM=（180°-∠FEG）①，

又，，

∴两式相加得∠AEN+∠BEM=2∠FEG+30°②，

由①②可得，（180°-∠FEG）=2∠FEG+30°，解得∠FEG=24°，

∴∠AEN+∠BEM =（180°-24°）=78°，
∴∠MEN=180°-（∠AEN+∠BEM） =180°-78°=102°．

故的度数为24°，的度数为102°.
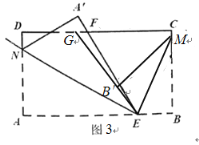
（3）如图3，若点G在点F的左侧，∠FEG=α．

根据（2）知，∠MEN=180°-（AEN+∠BEM）=180°-（∠AEF+∠BEG）=180°-(180°+∠FEG)=90°-∠FEG．

∴∠MEN=90°-α．