题目内容
把抛物线y=-x2向左平移1个单位,然后向上平移3个单位,则平移后的抛物线的解析式为
- A.y=-(x-1)2-3
- B.y=-(x+1)2-3
- C.y=-(x-1)2+3
- D.y=-(x+1)2+3
D
解析:
分析:根据平移不改变抛物线的形状,平移后抛物线的解析式中a的值不变.抛物线y=-x2的顶点坐标为(0,0),平移后抛物线的顶点坐标为(-1,3).所以平移后抛物线的解析式为y=-(x+1)2+3.解:D.
点评:任意二次函数y=ax2+bx+c(a≠0,a、b、c是常数)都可以转化为y=a(x-h)2+k的形式,因此可以由y=ax2经过平移得到,具体做法是将y=ax2的图象向右(h>0)(向左(h<0))平移|h|个单位,并向上(k>0)(向下(k<0))平移|k|个单位.
解析:
分析:根据平移不改变抛物线的形状,平移后抛物线的解析式中a的值不变.抛物线y=-x2的顶点坐标为(0,0),平移后抛物线的顶点坐标为(-1,3).所以平移后抛物线的解析式为y=-(x+1)2+3.解:D.
点评:任意二次函数y=ax2+bx+c(a≠0,a、b、c是常数)都可以转化为y=a(x-h)2+k的形式,因此可以由y=ax2经过平移得到,具体做法是将y=ax2的图象向右(h>0)(向左(h<0))平移|h|个单位,并向上(k>0)(向下(k<0))平移|k|个单位.

练习册系列答案
相关题目
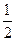 x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是 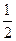 x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是 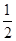 x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
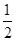 x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是