题目内容
如图所示，大正方形ABCD的两个对角上摆放着两个小正方形BEFG和DHMN．两个小正方形重迭部分的面积是1．A、F、N三点共线，如果ABCD的面积是144，那么MN=4
4
．分析：设MN=y，EF=x，则x+y=12+1，根据相似三角形列出关于x，y的等量关系式并求解，
解答：解：设MN=y，EF=x，
则x+y=12+1=13，得到x=13-y①，
∵
=
，即
=
②，
把①代入②消去x整理得：
y2-y-12=0，
计算得y=4或y=-3（舍去），
即MN=4．
故答案为：4．
则x+y=12+1=13，得到x=13-y①，
∵
| EF |
| AD |
| AE |
| DN |
| x |
| 12 |
| 12-x |
| y |
把①代入②消去x整理得：
y2-y-12=0，
计算得y=4或y=-3（舍去），
即MN=4．
故答案为：4．
点评：本题考查了相似三角形对应边比例相等的性质，考查了正方形各内角均为90°的性质，考查了一元二次方程的求解．
解本题的关键是找到相似三角形，并且根据对应边比值相等列出等量关系式进行求解．
解本题的关键是找到相似三角形，并且根据对应边比值相等列出等量关系式进行求解．
练习册系列答案
相关题目
10、用四个全等的矩形和一个小正方形拼成如图所示的大正方形，已知大正方形的面积是144，小正方形的面积是4，若用x，y表示矩形的长和宽（x＞y），则下列关系式中不正确的是（ ）
四个相同的长方形和一个小正方形拼成如图所示的大正方形，已知大正方形的面积是144，小正方形的面积是4，若用x、y表示长方形的长和宽，则小长方形的长为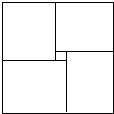
某同学想用5个边长不等的正方形，拼成如图所示的大正方形．请问该同学的想法能实现吗？如果能实现，试求这5个正方形的边长；如果不能，请说明理由．
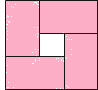用四个完全一样的长方形（长、宽分别设为x、y）拼成如图所示的大正方形，已知大正方形的面积为36，中间空缺的小正方形的面积为4，则下列关系式中不正确的是（ ）