题目内容
若x1、x2都满足条件|2x-1|+|2x+3|=4且x1<x2,则x1-x2的取值范围是________
-2≤x1-x2<0
分析:根据|2x-1|+|2x+3|=4,两边都除以2得: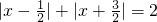 ,然后借助数轴进行解题.
,然后借助数轴进行解题.
解答:|2x-1|+|2x+3|=4,两边都除以2得:
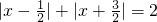 .
.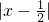 ,|x-
,|x- |表示数轴上数x的点到
|表示数轴上数x的点到 的点之间的距离,
的点之间的距离,
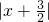 表示数轴上表示数x的点到表示数-
表示数轴上表示数x的点到表示数- 点之间的距离,
点之间的距离,
显然,当 或
或 时,
时,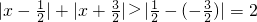 ,
,
而当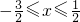 时,
时,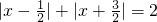 ,又x1<x2,
,又x1<x2,
∴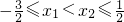 ,∵-
,∵- ≤x2
≤x2 ,
,
∴- ≤-x2≤
≤-x2≤ ,-
,- ≤x1
≤x1 ,
,
上面两式相加:故-2≤x1-x2≤2,
又∵x1<x2,∴x1-x2<0,
故答案为:-2≤x1-x2<0.
点评:本题考查了含绝对值符号的一元一次方程,难度适中,关键是借助数轴的思想解题,从而可简化运算.
分析:根据|2x-1|+|2x+3|=4,两边都除以2得:
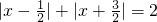 ,然后借助数轴进行解题.
,然后借助数轴进行解题.解答:|2x-1|+|2x+3|=4,两边都除以2得:
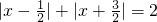 .
.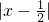 ,|x-
,|x- |表示数轴上数x的点到
|表示数轴上数x的点到 的点之间的距离,
的点之间的距离,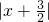 表示数轴上表示数x的点到表示数-
表示数轴上表示数x的点到表示数- 点之间的距离,
点之间的距离,显然,当
 或
或 时,
时,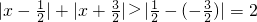 ,
,而当
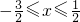 时,
时,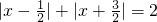 ,又x1<x2,
,又x1<x2,∴
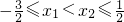 ,∵-
,∵- ≤x2
≤x2 ,
,∴-
 ≤-x2≤
≤-x2≤ ,-
,- ≤x1
≤x1 ,
,上面两式相加:故-2≤x1-x2≤2,
又∵x1<x2,∴x1-x2<0,
故答案为:-2≤x1-x2<0.
点评:本题考查了含绝对值符号的一元一次方程,难度适中,关键是借助数轴的思想解题,从而可简化运算.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.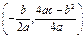 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线. ,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.