题目内容
【题目】根据下列条件求函数的表达式：
（1）已知变量x，y，t满足：y＝t2﹣2，x＝3﹣t．求y关于x的函数表达式；
（2）已知二次函数y＝ax2+bx+c，当x＝1时，y＝2；当x＝﹣2时，y＝﹣7；当x＝﹣1时，y＝0．求这个二次函数的表达式．
【答案】（1）y＝x2﹣6x+7；（2）y＝﹣2x2+x+3．
【解析】
（1）直接利用y，x与t的关系得出y与x之间的关系；
（2）直接利用待定系数法得出二次函数表达式．
解：（1）∵y＝t2﹣2，x＝3﹣t，
x2=（3﹣t）2＝t2﹣6t+9，
∴y＝x2+6t﹣11＝x2﹣6（3﹣t）+7
＝x2﹣6x+7；
（2）把x＝1，y＝2；x＝﹣2，y＝﹣7；x＝﹣1，y＝0分别代入原式得：
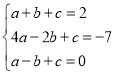，解得：
，
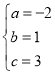故这个二次函数的表达式为：y＝﹣2x2+x+3．
练习册系列答案
相关题目
