题目内容
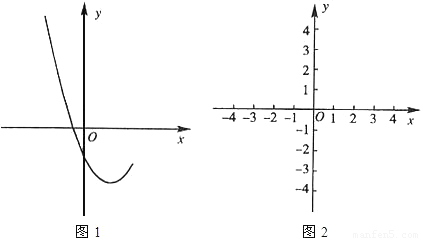
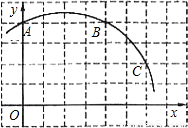
(2006•海淀区)已知抛物线y1=x2-2x+c的部分图象如图1所示.(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线y1=x2-2x+c的解析式;
(3)若反比例函数
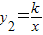 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小.
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小.
【答案】分析:(1)根据图1中抛物线的图象可知:c<0且抛物线与x轴应该有两个交点,因此△>0,由此可求出c的取值范围.
(2)将点(0,-1)的坐标代入抛物线中即可得出函数的解析式.
(3)求两图象交点是一个难点,两图象交点即为两图象所对应解析式构成方程组的解,观察图象,y1与y2除交点(1,-2)外,还有两个交点大致为(-1,2)和(2,-1),把x=-1,y=2和x=2,y=-1分别代入y1=x2-2x-1和y2= 可知,(-1,2)和(2,-1)是y1与y2的两个交点.根据图象可知:当x<-1或0<x<1或x>2时,y1>y2,当x=-1或x=1或x=2时,y1=y2,当-1<x<0或1<x<2时,y2>y1.
可知,(-1,2)和(2,-1)是y1与y2的两个交点.根据图象可知:当x<-1或0<x<1或x>2时,y1>y2,当x=-1或x=1或x=2时,y1=y2,当-1<x<0或1<x<2时,y2>y1.
解答: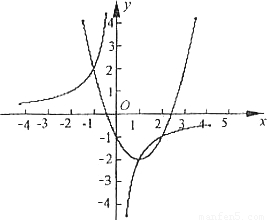 解:(1)根据图象可知c<0
解:(1)根据图象可知c<0
且抛物线y1=x2-2x+c与x轴有两个交点
所以一元二次方程x2-2x+c=0有两个不等的实数根.
所以△=(-2)2-4c=4-4c>0,且c<0
所以c<0.
(2)因为抛物线经过点(0,-1)
把x=0,y1=-1代入y1=x2-2x+c
得c=-1
故所求抛物线的解析式为y1=x2-2x-1
(3)因为反比例函数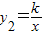 的图象经过抛物线y1=x2-2x-1上的点(1,a)
的图象经过抛物线y1=x2-2x-1上的点(1,a)
把x=1,y1=a代入y1=x2-2x-1,得a=-2
把x=1,a=-2代入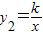 ,得k=-2
,得k=-2
所以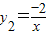
画出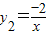 的图象如图所示.
的图象如图所示.
观察图象,y1与y2除交点(1,-2)外,还有两个交点大致为(-1,2)和(2,-1)
把x=-1,y2=2和x=2,y2=-1;
分别代入y1=x2-2x-1和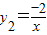 可知:
可知:
(-1,2)和(2,-1)是y1与y2的两个交点
根据图象可知:当x<-1或0<x<1或x>2时,y1>y2
当x=-1或x=1或x=2时,y1=y2
当-1<x<0或1<x<2时,y2>y1.
点评:本题考查二次函数、反比例函数、一元二次方程根的判别式等知识,是一道综合题,第(3)小题考查了学生的作图和探究能力,属于中难度题.
(2)将点(0,-1)的坐标代入抛物线中即可得出函数的解析式.
(3)求两图象交点是一个难点,两图象交点即为两图象所对应解析式构成方程组的解,观察图象,y1与y2除交点(1,-2)外,还有两个交点大致为(-1,2)和(2,-1),把x=-1,y=2和x=2,y=-1分别代入y1=x2-2x-1和y2=
 可知,(-1,2)和(2,-1)是y1与y2的两个交点.根据图象可知:当x<-1或0<x<1或x>2时,y1>y2,当x=-1或x=1或x=2时,y1=y2,当-1<x<0或1<x<2时,y2>y1.
可知,(-1,2)和(2,-1)是y1与y2的两个交点.根据图象可知:当x<-1或0<x<1或x>2时,y1>y2,当x=-1或x=1或x=2时,y1=y2,当-1<x<0或1<x<2时,y2>y1.解答:
 解:(1)根据图象可知c<0
解:(1)根据图象可知c<0且抛物线y1=x2-2x+c与x轴有两个交点
所以一元二次方程x2-2x+c=0有两个不等的实数根.
所以△=(-2)2-4c=4-4c>0,且c<0
所以c<0.
(2)因为抛物线经过点(0,-1)
把x=0,y1=-1代入y1=x2-2x+c
得c=-1
故所求抛物线的解析式为y1=x2-2x-1
(3)因为反比例函数
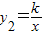 的图象经过抛物线y1=x2-2x-1上的点(1,a)
的图象经过抛物线y1=x2-2x-1上的点(1,a)把x=1,y1=a代入y1=x2-2x-1,得a=-2
把x=1,a=-2代入
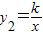 ,得k=-2
,得k=-2所以
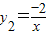
画出
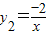 的图象如图所示.
的图象如图所示.观察图象,y1与y2除交点(1,-2)外,还有两个交点大致为(-1,2)和(2,-1)
把x=-1,y2=2和x=2,y2=-1;
分别代入y1=x2-2x-1和
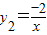 可知:
可知:(-1,2)和(2,-1)是y1与y2的两个交点
根据图象可知:当x<-1或0<x<1或x>2时,y1>y2
当x=-1或x=1或x=2时,y1=y2
当-1<x<0或1<x<2时,y2>y1.
点评:本题考查二次函数、反比例函数、一元二次方程根的判别式等知识,是一道综合题,第(3)小题考查了学生的作图和探究能力,属于中难度题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
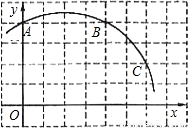
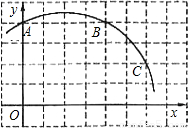
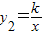 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小.
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小.