题目内容
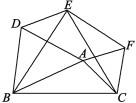
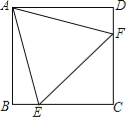
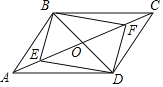
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:四边形![]() 为矩形;
为矩形;
(2)判断四边形![]() 是什么特殊四边形?并说明理由;
是什么特殊四边形?并说明理由;
(3)求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)四边形EFPH为矩形,理由见解析;(3)![]()
【解析】
(1)由平行线的性质证出∠BCD=90°即可;
(2)根据矩形性质得出CD=2,根据勾股定理求出CE和BE,求出CE2+BE2的值,求出BC2,根据勾股定理的逆定理求出∠BEC=90°,根据矩形的性质和平行四边形的判定,推出平行四边形DEBP和AECP,推出EH//FP,EF//HP,推出平行四边形EFPH,根据矩形的判定推出即可;
(3)根据三角形的面积公式求出CF,求出EF,根据勾股定理求出PF,根据面积公式求出即可.
(1)证明:∵AB//CD,
∴∠CBA+∠BCD=180°,
∵∠CBA=∠ADC=90°,
∴∠BCD=90°,
∴四边形ABCD是矩形;
(2)解:四边形EFPH为矩形;理由如下:
∵四边形ABCD是矩形,
∴AD=BC=5,AB=CD=2,AD∥BC,
由勾股定理得:CE= ![]() ,
,
同理BE=2![]() ,
,
∴CE2+BE2=5+20=25,
∵BC2=52=25,
∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.
∵DE=BP,DE//BP,
∴四边形DEBP是平行四边形,
∴BE//DP,
∵AD=BC,AD//BC,DE=BP,
∴AE=CP,
∴四边形AECP是平行四边形,
∴AP//CE,
∴四边形EFPH是平行四边形,
∵∠BEC=90°,
∴平行四边形EFPH是矩形.
(3)解:∵四边形AECP是平行四边形,
∴PD=BE=2![]() ,
,
在Rt△PCD中,FC⊥PD,PC=BC-BP=4,
由三角形的面积公式得:![]() PDCF=
PDCF=![]() PCCD,
PCCD,
∴CF=![]() ,
,
∴EF=CE-CF=![]() ,
,
∵PF=![]() ,
,
∴S矩形EFPH=EFPF=![]() ,
,
即:四边形EFPH的面积是![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】近日,中国工程院院士、“杂交水稻之父”袁隆平团队选育培植的耐盐碱水稻(即海水稻)在山东青岛等六个试验基地开始春播育秧,预计今年的种植规模将超一万亩.已知去年某基地甲、乙两块实验田海水稻的总产量都是3600千克,乙实验田海水稻种植面积是甲实验田的![]() ,而乙实验田海水稻平均亩产量比甲多60千克.
,而乙实验田海水稻平均亩产量比甲多60千克.
(1)求甲、乙两块实验田种植海水稻的面积;
(2)经过科学家的努力,海水稻正从试验田走向餐桌,某电商新购进A、B两种包装的海水稻产品共50袋,其进价、标价及优惠方案如下表所示.若要保证这批海水稻产品全部售出后所得利润不少于1000元,该电商至少要购进A种包装的海水稻产品多少袋?
包装类型 | A | B |
进价(元/袋) | 100 | 30 |
标价(元/袋) | 150 | 50 |
优惠方案 | 全部九折 | |