题目内容
 如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.
如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.
解:由已知:AB∥OP,
∴△ABC∽△OPC.
∵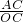 =
= ,
,
∵OP=l,AB=h,OA=a,
∴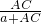 =
=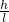 ,
,
∴解得:AC= .
.
分析:根据AB∥OP可以得到△ABC∽△OPC,然后可以得到比例式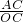 =
= ,然后代入数据即可得到结论;
,然后代入数据即可得到结论;
点评:本题考查了相似三角形的应用,是把实际问题转化成相似三角形的问题,然后利用相似三角形对应边成比例解题.
∴△ABC∽△OPC.
∵
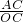 =
= ,
,∵OP=l,AB=h,OA=a,
∴
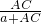 =
=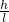 ,
,∴解得:AC=
 .
.分析:根据AB∥OP可以得到△ABC∽△OPC,然后可以得到比例式
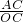 =
= ,然后代入数据即可得到结论;
,然后代入数据即可得到结论;点评:本题考查了相似三角形的应用,是把实际问题转化成相似三角形的问题,然后利用相似三角形对应边成比例解题.

练习册系列答案
相关题目
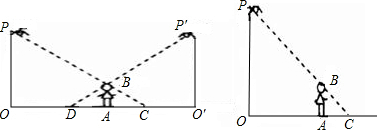
 如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.
如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.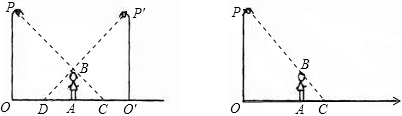
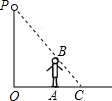 如图,李华晚上在路灯下散步,已知李华的身高AB=h,灯柱的高OP=l,李华距灯柱OP的水平距离OA=a.
如图,李华晚上在路灯下散步,已知李华的身高AB=h,灯柱的高OP=l,李华距灯柱OP的水平距离OA=a.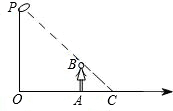 如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为
如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为