题目内容
设a2+2a-1=0,b4―2b2―1=0,且1-ab2≠0,则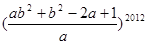 =__________.
=__________.
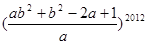 =__________.
=__________.1
∵a2+2a-1=0,b4-2b2-1=0∴(a2+2a-1)-(b4-2b2-1)=0
化简之后得到:(a+b2)(a-b2+2)=0
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0
因此a+b2=0,即b2="-a" ∴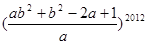 =
=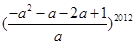 =(-1)2012=1.
=(-1)2012=1.
化简之后得到:(a+b2)(a-b2+2)=0
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0
因此a+b2=0,即b2="-a" ∴
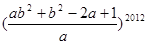 =
=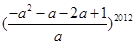 =(-1)2012=1.
=(-1)2012=1.
练习册系列答案
相关题目
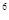 ÷a
÷a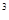 =a
=a

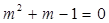 ,则
,则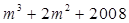 的值为( )
的值为( )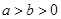 ,
, ,则
,则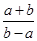 的值等于 .
的值等于 .